1. Introduction
Convex and concave functions play an important role in statistics, probability, and especially in reliability theory, wherein they lead to some useful inequalities. Many aspects of these functions have been studied in detail in different contexts and we refer the readers to the classical monographs [Reference Barlow and Proschan5, Reference Dharmadhikari and Joag-Dev6, Reference Marshall and Olkin16]. In this note, we derive a simple integral inequality for log-concave functions and then demonstrate its application in examining the monotonicity of failure rates.
A measurable function ![]() $f: {\mathbb{R}} \to {\mathbb{R}}_+$ is said to be log-concave if:
$f: {\mathbb{R}} \to {\mathbb{R}}_+$ is said to be log-concave if:
for all ![]() $x,y \in {\mathbb{R}}$ and
$x,y \in {\mathbb{R}}$ and ![]() $t \in (0,1)$. It is easy to see that the support of a log-concave function is an interval and that the above definition amounts to the concavity on
$t \in (0,1)$. It is easy to see that the support of a log-concave function is an interval and that the above definition amounts to the concavity on ![]() ${\mathbb{R}}$ of the function
${\mathbb{R}}$ of the function ![]() $\log f : {\mathbb{R}}\to{\mathbb{R}}\cup\{-\infty\}$ with possible value
$\log f : {\mathbb{R}}\to{\mathbb{R}}\cup\{-\infty\}$ with possible value ![]() $-\infty$ outside Supp f. Interested readers may refer to [Reference Saumard and Wellner19] for a recent survey on log-concave functions and relevant topics in statistics.
$-\infty$ outside Supp f. Interested readers may refer to [Reference Saumard and Wellner19] for a recent survey on log-concave functions and relevant topics in statistics.
A function ![]() $f: {\mathbb{R}}_+ \to {\mathbb{R}}_+$ is said to be hyperbolically monotone if the function
$f: {\mathbb{R}}_+ \to {\mathbb{R}}_+$ is said to be hyperbolically monotone if the function ![]() $x\mapsto f(e^x)$ is log-concave on
$x\mapsto f(e^x)$ is log-concave on ![]() ${\mathbb{R}}$; see, for example, Section 9.2 in [Reference Saumard and Wellner19] and the references therein for more information on this notion. In Lemma 2.3 of [Reference Alimohammadi and Navarro2], a characterization of hyperbolic monotonicity is given as:
${\mathbb{R}}$; see, for example, Section 9.2 in [Reference Saumard and Wellner19] and the references therein for more information on this notion. In Lemma 2.3 of [Reference Alimohammadi and Navarro2], a characterization of hyperbolic monotonicity is given as:
for all ![]() $y\ge x \ge 0$ and
$y\ge x \ge 0$ and ![]() $c \geq 1.$ In [Reference Alimohammadi and Navarro2], this characterization has then utilized to study the preservation of increasing failure rate property under the formation of
$c \geq 1.$ In [Reference Alimohammadi and Navarro2], this characterization has then utilized to study the preservation of increasing failure rate property under the formation of ![]() $(n-k+1)$-out-of-n systems with discrete distributions. In this note, we give a short new proof of this preservation property by means of a characterization of hyperbolically monotone functions with an average version of the inequality in (1), holding without any restriction on
$(n-k+1)$-out-of-n systems with discrete distributions. In this note, we give a short new proof of this preservation property by means of a characterization of hyperbolically monotone functions with an average version of the inequality in (1), holding without any restriction on ![]() $x,y,c$. This result turns out to be a consequence of the integral characterization of log-concave functions presented in the following section:
$x,y,c$. This result turns out to be a consequence of the integral characterization of log-concave functions presented in the following section:
2. Main results
Theorem 2.1. Let ![]() $f : \mathbb{R} \to \mathbb{R}_+$ be continuous. Then, f is log-concave if and only if:
$f : \mathbb{R} \to \mathbb{R}_+$ be continuous. Then, f is log-concave if and only if:
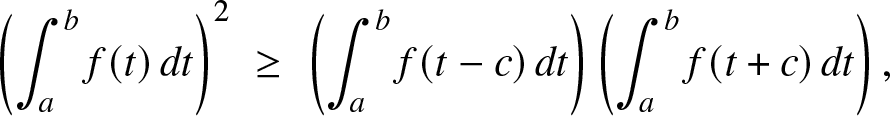 \begin{equation}
\left( \int_a^b f(t)\, dt\right)^2 \; \ge\; \left( \int_a^b f(t-c)\, dt\right)\left( \int_a^b f(t+c)\, dt\right),
\end{equation}
\begin{equation}
\left( \int_a^b f(t)\, dt\right)^2 \; \ge\; \left( \int_a^b f(t-c)\, dt\right)\left( \int_a^b f(t+c)\, dt\right),
\end{equation}for all a < b and c > 0.
Proof. The if part follows by midpoint convexity. Fix ![]() $a \in{\mathbb{R}}$ and c > 0. Dividing both sides of (2) by
$a \in{\mathbb{R}}$ and c > 0. Dividing both sides of (2) by ![]() $(b-a)^2$ and letting
$(b-a)^2$ and letting ![]() $b\downarrow a,$ we obtain:
$b\downarrow a,$ we obtain:
by continuity of ![]() $f.$ This implies that Supp
$f.$ This implies that Supp ![]() $f\, =\, \{x\in{\mathbb{R}}, \;\; f(x)\neq 0\}$ is an interval, which we denote by
$f\, =\, \{x\in{\mathbb{R}}, \;\; f(x)\neq 0\}$ is an interval, which we denote by ![]() $I.$ Setting
$I.$ Setting ![]() $x= a-c, y = a+c$ and
$x= a-c, y = a+c$ and ![]() $g =\log f,$ we get:
$g =\log f,$ we get:
 \begin{equation*}\frac{g(x)\, +\, g(y)}{2} \; \le\; g \left( \frac{x+y}{2}\right),\end{equation*}
\begin{equation*}\frac{g(x)\, +\, g(y)}{2} \; \le\; g \left( \frac{x+y}{2}\right),\end{equation*} for all ![]() $x,y \in I.$ This shows that g is midpoint concave in I and, by Sierpiński’s theorem—see [Reference Donoghue7], p. 12, that it is concave in
$x,y \in I.$ This shows that g is midpoint concave in I and, by Sierpiński’s theorem—see [Reference Donoghue7], p. 12, that it is concave in ![]() $I,$ hence also on the whole
$I,$ hence also on the whole ![]() ${\mathbb{R}}$ since
${\mathbb{R}}$ since ![]() $g = -\infty$ outside
$g = -\infty$ outside ![]() $I.$
$I.$
For the only if part, we need to show that:
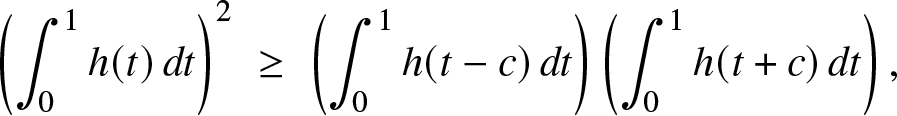 \begin{equation}\left( \int_0^1 h(t)\, dt\right)^2 \; \ge\; \left( \int_0^1 h(t-c)\, dt\right)\left( \int_0^1 h(t+c)\, dt\right),
\end{equation}
\begin{equation}\left( \int_0^1 h(t)\, dt\right)^2 \; \ge\; \left( \int_0^1 h(t-c)\, dt\right)\left( \int_0^1 h(t+c)\, dt\right),
\end{equation} for all ![]() $c \gt 0,$ wherein we have set
$c \gt 0,$ wherein we have set ![]() $h(t) = f(a + t(b-a))$ which is a log-concave function on
$h(t) = f(a + t(b-a))$ which is a log-concave function on ![]() ${\mathbb{R}}.$ We will present three different proofs. In the first one, we show that the mapping:
${\mathbb{R}}.$ We will present three different proofs. In the first one, we show that the mapping:
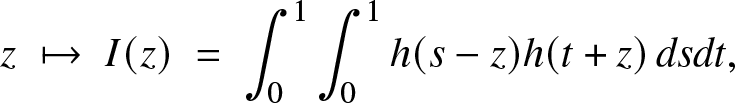 \begin{equation*}z\;\mapsto\;I(z)\;=\;\int_0^1\int_0^1 h(s-z)h(t+z)\, ds dt,\end{equation*}
\begin{equation*}z\;\mapsto\;I(z)\;=\;\int_0^1\int_0^1 h(s-z)h(t+z)\, ds dt,\end{equation*} is non-increasing in ![]() $(0,\infty).$ Then, by making the change of variables
$(0,\infty).$ Then, by making the change of variables ![]() $s=u-v$ and
$s=u-v$ and ![]() $t=u+v$, we have the decomposition
$t=u+v$, we have the decomposition ![]() $I(z)=2(I_1(z)+I_2(z))$, with:
$I(z)=2(I_1(z)+I_2(z))$, with:
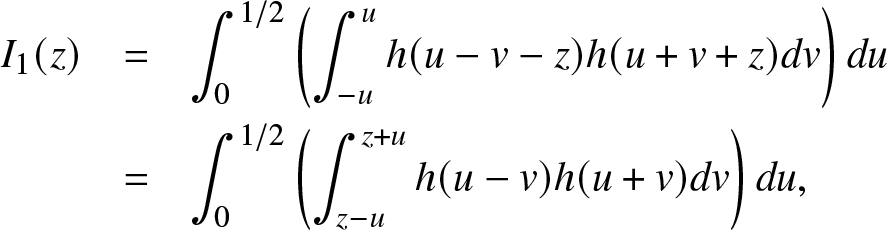 \begin{eqnarray*}
I_1(z) & = & \int_0^{1/2}\left( \int_{-u}^{u}h(u-v-z)h(u+v+z)dv\right) du\\
& = & \int_0^{1/2}\left( \int_{z-u}^{z+u}h(u-v)h(u+v)dv\right) du,
\end{eqnarray*}
\begin{eqnarray*}
I_1(z) & = & \int_0^{1/2}\left( \int_{-u}^{u}h(u-v-z)h(u+v+z)dv\right) du\\
& = & \int_0^{1/2}\left( \int_{z-u}^{z+u}h(u-v)h(u+v)dv\right) du,
\end{eqnarray*}and
 \begin{eqnarray*}
I_2(z) & = & \int_{1/2}^1\left( \int_{u-1}^{1-u}h(u-v-z)h(u+v+z)dv\right) du\\
& = & \int_{1/2}^1\left( \int_{u-1+z}^{1-u+z}h(u-v)h(u+v)dv\right) du.
\end{eqnarray*}
\begin{eqnarray*}
I_2(z) & = & \int_{1/2}^1\left( \int_{u-1}^{1-u}h(u-v-z)h(u+v+z)dv\right) du\\
& = & \int_{1/2}^1\left( \int_{u-1+z}^{1-u+z}h(u-v)h(u+v)dv\right) du.
\end{eqnarray*} By the continuity of ![]() $h,$ we can differentiate under the integral and obtain:
$h,$ we can differentiate under the integral and obtain:
 \begin{equation*}I_1'(z)\;=\;\int_0^{1/2} \left( h(-z)h(2u+z) - h(2u- z)h(z)\right)\, du\;\le\; 0,\end{equation*}
\begin{equation*}I_1'(z)\;=\;\int_0^{1/2} \left( h(-z)h(2u+z) - h(2u- z)h(z)\right)\, du\;\le\; 0,\end{equation*} where the inequality comes from Eq. (2) in [Reference An3] with ![]() $- z=x_1 \leq x_2=2u- z$ and
$- z=x_1 \leq x_2=2u- z$ and ![]() $\delta=2z$. Similarly, we obtain:
$\delta=2z$. Similarly, we obtain:
 \begin{equation*}I_2'(z)\; =\; \int_{1/2}^1 \left( h(2u-1-z)h(1+z) - h(-z)h(2u+ z)\right)\, du\;\le\; 0,\end{equation*}
\begin{equation*}I_2'(z)\; =\; \int_{1/2}^1 \left( h(2u-1-z)h(1+z) - h(-z)h(2u+ z)\right)\, du\;\le\; 0,\end{equation*} with ![]() $2u - 1- z=x_1 \leq x_2=1 - z$ and again
$2u - 1- z=x_1 \leq x_2=1 - z$ and again ![]() $\delta=2z$. This completes the proof of the theorem.
$\delta=2z$. This completes the proof of the theorem.
The second proof relies on discretization. For all ![]() $p,N \ge 1,$ the non-negative sequences
$p,N \ge 1,$ the non-negative sequences ![]() $\{a_n, n\ge 0\}$ and
$\{a_n, n\ge 0\}$ and ![]() $\{b_n, n\ge 0\}$, defined by:
$\{b_n, n\ge 0\}$, defined by:
are such that ![]() $a_j b_k \ge b_j a_k$ for all
$a_j b_k \ge b_j a_k$ for all ![]() $k\ge j\ge 0$ by the log-concavity of h and appealing again to Eq. (2) in [Reference An3]. It is then easy to see that this implies:
$k\ge j\ge 0$ by the log-concavity of h and appealing again to Eq. (2) in [Reference An3]. It is then easy to see that this implies:
Fix now c > 0 and choose an integer ![]() $p= p_N$ such that
$p= p_N$ such that ![]() $N^{-1}p_N \to c$ as
$N^{-1}p_N \to c$ as ![]() $N\to\infty.$ Multiplying by N −2 and letting
$N\to\infty.$ Multiplying by N −2 and letting ![]() $N\to\infty$ in (4), by Riemann approximation, we obtain the required inequality in (3).
$N\to\infty$ in (4), by Riemann approximation, we obtain the required inequality in (3).
The third proof is more conceptual and hinges upon the Prékopa-Leindler inequality. Let µ be a positive measure on ![]() ${\mathbb{R}}^2$ with density
${\mathbb{R}}^2$ with density ![]() $g(x,y) = h(x) h(y).$ As g is log-concave on
$g(x,y) = h(x) h(y).$ As g is log-concave on ![]() ${\mathbb{R}}^2,$ the Prékopa-Leindler inequality (see Theorem 1.1 in [Reference Maurey17]) implies that
${\mathbb{R}}^2,$ the Prékopa-Leindler inequality (see Theorem 1.1 in [Reference Maurey17]) implies that ![]() $\mu(tA + (1-t) B) \ge \mu(A)^t \mu(B)^{1-t}$ for all
$\mu(tA + (1-t) B) \ge \mu(A)^t \mu(B)^{1-t}$ for all ![]() $t\in (0,1)$ and
$t\in (0,1)$ and ![]() $A,B\subset{\mathbb{R}}^2$ measurable where, here and throughout, we have used the standard Minkowski notation:
$A,B\subset{\mathbb{R}}^2$ measurable where, here and throughout, we have used the standard Minkowski notation:
Now, upon setting ![]() $A = [0,1]^2$ and
$A = [0,1]^2$ and ![]() $z = (c,c)\in{\mathbb{R}}^2$, we have,
$z = (c,c)\in{\mathbb{R}}^2$, we have,
 \begin{equation*}A\; = \frac{1}{2} (A-z) + \frac{1}{2} (A+z),\end{equation*}
\begin{equation*}A\; = \frac{1}{2} (A-z) + \frac{1}{2} (A+z),\end{equation*} by the convexity of ![]() $A.$ This implies
$A.$ This implies
 \begin{equation*}\left( \int_0^1 h(t)\, dt\right)^2\; =\;\mu(A)\; =\;\mu\left( \frac{1}{2} (A-z) + \frac{1}{2} (A+z)\right) \; \ge\; \sqrt{\mu(A-z)\mu(A+z)},\end{equation*}
\begin{equation*}\left( \int_0^1 h(t)\, dt\right)^2\; =\;\mu(A)\; =\;\mu\left( \frac{1}{2} (A-z) + \frac{1}{2} (A+z)\right) \; \ge\; \sqrt{\mu(A-z)\mu(A+z)},\end{equation*}with
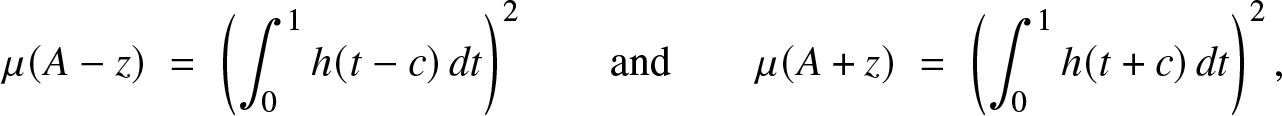 \begin{equation*}\mu(A-z)\; =\; \left(\int_0^1 h(t-c)\,dt\right)^2\qquad\mbox{and}\qquad \mu(A+z)\; =\; \left(\int_0^1 h(t+c)\,dt\right)^2,\end{equation*}
\begin{equation*}\mu(A-z)\; =\; \left(\int_0^1 h(t-c)\,dt\right)^2\qquad\mbox{and}\qquad \mu(A+z)\; =\; \left(\int_0^1 h(t+c)\,dt\right)^2,\end{equation*}which implies the inequality in (3).
Remark 2.2. (a) Above, the continuity condition is not necessary and can be relaxed. Indeed, the proof of the only if part relies only on log-concavity, and for the if part, we used Sierpinśki’s theorem, which holds under a sole measurability assumption. On the other hand, the argument for the if part also uses:
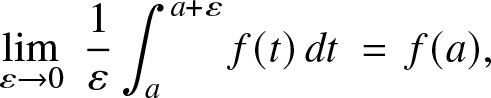 \begin{equation}
\lim_{\varepsilon\to 0}\; \frac{1}{\varepsilon} \int_a^{a+\varepsilon} f(t) \, dt\; =\; f(a),
\end{equation}
\begin{equation}
\lim_{\varepsilon\to 0}\; \frac{1}{\varepsilon} \int_a^{a+\varepsilon} f(t) \, dt\; =\; f(a),
\end{equation} for all ![]() $a\in{\mathbb{R}},$ which may fail if f is assumed only to be measurable. Observe that (5) means that every real number is a so-called Lebesgue density point for
$a\in{\mathbb{R}},$ which may fail if f is assumed only to be measurable. Observe that (5) means that every real number is a so-called Lebesgue density point for ![]() $f,$ which holds true, for example, when f is right-continuous;
$f,$ which holds true, for example, when f is right-continuous;
(b) The mid-convexity argument and the Prékopa-Leindler inequality remain true in ![]() ${\mathbb{R}}^{2d}$. Then, they imply the following multidimensional generalization: a continuous function
${\mathbb{R}}^{2d}$. Then, they imply the following multidimensional generalization: a continuous function ![]() $f : {\mathbb{R}}^d\to{\mathbb{R}}^+$ is log-concave if:
$f : {\mathbb{R}}^d\to{\mathbb{R}}^+$ is log-concave if:
 \begin{equation*}\left(\int_{A} f(t)\, dt\right)^2 \; \ge\; \left(\int_{A} f(t-x)\, dt\right)\,\times\, \left(\int_{A} f(t+x)\, dt\right)\end{equation*}
\begin{equation*}\left(\int_{A} f(t)\, dt\right)^2 \; \ge\; \left(\int_{A} f(t-x)\, dt\right)\,\times\, \left(\int_{A} f(t+x)\, dt\right)\end{equation*} for every ![]() $A\subset{\mathbb{R}}^d$ measurable and every
$A\subset{\mathbb{R}}^d$ measurable and every ![]() $x\in{\mathbb{R}}^d$;
$x\in{\mathbb{R}}^d$;
(c) Using either the first or the second proof for the only if part, we can show similarly that for a continuous function ![]() $f :{\mathbb{R}}\to{\mathbb{R}}^+,$ the log-convexity of f on its support is equivalent to:
$f :{\mathbb{R}}\to{\mathbb{R}}^+,$ the log-convexity of f on its support is equivalent to:
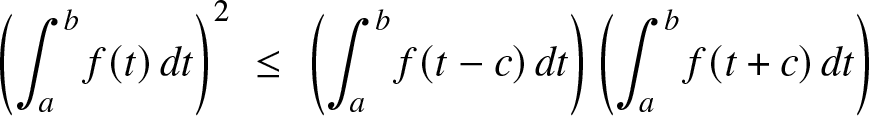 \begin{equation*}\left( \int_a^b f(t)\, dt\right)^2 \; \le\; \left(\int_a^b f(t-c)\, dt\right)\left( \int_a^b f(t+c)\, dt\right)\end{equation*}
\begin{equation*}\left( \int_a^b f(t)\, dt\right)^2 \; \le\; \left(\int_a^b f(t-c)\, dt\right)\left( \int_a^b f(t+c)\, dt\right)\end{equation*} for all a < b and c > 0 such that ![]() $a-c, b+c \in {\rm Supp} f.$ Notice that contrary to log-concavity, the support condition is important and that the characterization becomes untrue without this condition; see the end of Section 3.1 for further discussion.
$a-c, b+c \in {\rm Supp} f.$ Notice that contrary to log-concavity, the support condition is important and that the characterization becomes untrue without this condition; see the end of Section 3.1 for further discussion.
We now state the aforementioned characterization of hyperbolically monotone functions.
Corollary 2.3. Let ![]() $f : {\mathbb{R}}_+ \to {\mathbb{R}}_+$ be continuous. Then, the function
$f : {\mathbb{R}}_+ \to {\mathbb{R}}_+$ be continuous. Then, the function ![]() $x\mapsto f(e^x)$ is log-concave on
$x\mapsto f(e^x)$ is log-concave on ![]() ${\mathbb{R}}$ if and only if:
${\mathbb{R}}$ if and only if:
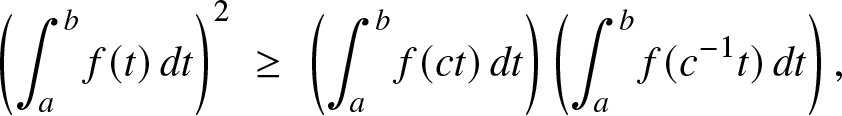 \begin{equation}
\left( \int_a^b f(t)\, dt\right)^2 \; \ge\; \left( \int_a^b f(ct)\, dt\right)\left( \int_a^b f(c^{-1} t)\, dt\right),
\end{equation}
\begin{equation}
\left( \int_a^b f(t)\, dt\right)^2 \; \ge\; \left( \int_a^b f(ct)\, dt\right)\left( \int_a^b f(c^{-1} t)\, dt\right),
\end{equation} for all ![]() $0 \lt a \lt b$ and c > 0.
$0 \lt a \lt b$ and c > 0.
Proof. Clearly, ![]() $x\mapsto f(e^x)$ is log-concave on
$x\mapsto f(e^x)$ is log-concave on ![]() ${\mathbb{R}}$ if and only if
${\mathbb{R}}$ if and only if ![]() $x\mapsto e^x f(e^x)$ is log-concave on
$x\mapsto e^x f(e^x)$ is log-concave on ![]() ${\mathbb{R}}$ which by Theorem 2.1 and some straightforward simplification, is equivalent to:
${\mathbb{R}}$ which by Theorem 2.1 and some straightforward simplification, is equivalent to:
 \begin{equation*} \left( \int_a^b e^t f(e^t)\, dt\right)^2 \; \ge\; \left(\int_a^b e^t f(ce^t)\, dt\right)\left( \int_a^b e^t f(c^{-1} e^t)\, dt\right),\end{equation*}
\begin{equation*} \left( \int_a^b e^t f(e^t)\, dt\right)^2 \; \ge\; \left(\int_a^b e^t f(ce^t)\, dt\right)\left( \int_a^b e^t f(c^{-1} e^t)\, dt\right),\end{equation*} for all a < b and c > 0. The result then follows readily from the change of variable ![]() $u = e^t.$
$u = e^t.$
Remark 2.4. In [Reference Kanter12], a related characterization of the log-concavity of ![]() $f(e^x)$ has been given as the “monotone likelihood property”. More precisely, the function
$f(e^x)$ has been given as the “monotone likelihood property”. More precisely, the function ![]() $x\mapsto f(e^x)$ is log-concave iff
$x\mapsto f(e^x)$ is log-concave iff ![]() $x\to f(x)/f(cx)$ is monotone on
$x\to f(x)/f(cx)$ is monotone on ![]() $(0,\infty)$ for every c > 0. In this regard, the characterization in (6), when rewritten as:
$(0,\infty)$ for every c > 0. In this regard, the characterization in (6), when rewritten as:
 \begin{equation*}\frac{{\displaystyle \int_a^b f(t)\, dt}}{{\displaystyle \int_a^b f(ct)\, dt}} \;\, \ge\;\, \frac{{\displaystyle \int_a^b f(c^{-1}t)\, dt}}{{\displaystyle \int_a^b f(t)\, dt}},\end{equation*}
\begin{equation*}\frac{{\displaystyle \int_a^b f(t)\, dt}}{{\displaystyle \int_a^b f(ct)\, dt}} \;\, \ge\;\, \frac{{\displaystyle \int_a^b f(c^{-1}t)\, dt}}{{\displaystyle \int_a^b f(t)\, dt}},\end{equation*}can be viewed as an “average monotone likelihood property.”
3. Applications to the study of failure rates
3.1. On increasing failure rates and proportional failure rates
Let X be a nonnegative variable with absolutely continuous cumulative distribution function F, survival function ![]() $\bar{F}=1-F$, and probability density function f. The function
$\bar{F}=1-F$, and probability density function f. The function ![]() $h=f/\bar F,$ known as the failure rate function of X, is an important measure used extensively in reliability, survival analysis and stochastic modeling. The function
$h=f/\bar F,$ known as the failure rate function of X, is an important measure used extensively in reliability, survival analysis and stochastic modeling. The function ![]() $x\mapsto xh(x)$ has been referred in [Reference Lariviere and Porteus15] as a generalized failure rate and in [Reference Righter, Shaked and Shanthikumar18] as a proportional failure rate. As a consequence of Theorem 2.1 and Corollary 2.3, we get a short proof for the following fact which is well-known for the function h (see [Reference Barlow and Proschan5, p. 76]) but less known for the function
$x\mapsto xh(x)$ has been referred in [Reference Lariviere and Porteus15] as a generalized failure rate and in [Reference Righter, Shaked and Shanthikumar18] as a proportional failure rate. As a consequence of Theorem 2.1 and Corollary 2.3, we get a short proof for the following fact which is well-known for the function h (see [Reference Barlow and Proschan5, p. 76]) but less known for the function ![]() $x\mapsto xh(x)$.
$x\mapsto xh(x)$.
Proposition 3.1. If f is log-concave, then h is non-decreasing. If ![]() $f(e^x)$ is log-concave, then
$f(e^x)$ is log-concave, then ![]() $x\mapsto xh(x)$ is non-decreasing.
$x\mapsto xh(x)$ is non-decreasing.
Proof. Suppose f is log-concave. Then, by taking ![]() $a=t \gt 0$ and letting
$a=t \gt 0$ and letting ![]() $b\to\infty$ in Theorem 2.1, we obtain:
$b\to\infty$ in Theorem 2.1, we obtain:
 \begin{eqnarray*}
\bar{F}^2(t)\; =\; \left(\int_{t}^{\infty} f(x)\, dx\right)^2\;\geq\;
\int_{t}^{\infty}\!\int_{t}^{\infty}f(x-c)f(y+c)\, dxdy\; =\; \bar{F}(t-c)\bar{F}(t+c),
\end{eqnarray*}
\begin{eqnarray*}
\bar{F}^2(t)\; =\; \left(\int_{t}^{\infty} f(x)\, dx\right)^2\;\geq\;
\int_{t}^{\infty}\!\int_{t}^{\infty}f(x-c)f(y+c)\, dxdy\; =\; \bar{F}(t-c)\bar{F}(t+c),
\end{eqnarray*} for all ![]() $c, t \gt 0.$ By mid-point convexity, this shows that
$c, t \gt 0.$ By mid-point convexity, this shows that ![]() $\bar{F}(x)$ is log-concave, or equivalently,
$\bar{F}(x)$ is log-concave, or equivalently,
 \begin{equation*}\frac{d}{dx}\ln(\bar{F}(x))\;=\; -\frac{f(x)}{\bar{F}(x)}\; =\; -h(x),\end{equation*}
\begin{equation*}\frac{d}{dx}\ln(\bar{F}(x))\;=\; -\frac{f(x)}{\bar{F}(x)}\; =\; -h(x),\end{equation*}is non-increasing, as required. The proof of the second part is analogous upon using:
 \begin{eqnarray*}
\bar{F}^2(t)\; =\; \left(\int_{t}^{\infty} f(x)\, dx\right)^2\;\geq\;
\int_{t}^{\infty}\!\int_{t}^{\infty}f(cx)f(c^{-1} y)\, dxdy\; =\; \bar{F}(ct)\bar{F}(c^{-1} t),
\end{eqnarray*}
\begin{eqnarray*}
\bar{F}^2(t)\; =\; \left(\int_{t}^{\infty} f(x)\, dx\right)^2\;\geq\;
\int_{t}^{\infty}\!\int_{t}^{\infty}f(cx)f(c^{-1} y)\, dxdy\; =\; \bar{F}(ct)\bar{F}(c^{-1} t),
\end{eqnarray*} for all ![]() $c, t \gt 0,$ which is obtained by taking
$c, t \gt 0,$ which is obtained by taking ![]() $a=t \gt 0$ and letting
$a=t \gt 0$ and letting ![]() $b\to\infty$ in Corollary 2.3.
$b\to\infty$ in Corollary 2.3.
In the above statement, we have used the fact that the non-decreasing property of h (resp. ![]() $x\mapsto xh(x)$) is equivalent to the log-concavity of
$x\mapsto xh(x)$) is equivalent to the log-concavity of ![]() ${\bar F}$ (resp.
${\bar F}$ (resp. ![]() $x\mapsto {\bar F}(e^x)$). The following example demonstrates a situation wherein this is also equivalent to the log-concavity of f (resp.
$x\mapsto {\bar F}(e^x)$). The following example demonstrates a situation wherein this is also equivalent to the log-concavity of f (resp. ![]() $x\mapsto f(e^x)$).
$x\mapsto f(e^x)$).
Example 3.2. Suppose X has the generalized gamma distribution with density:
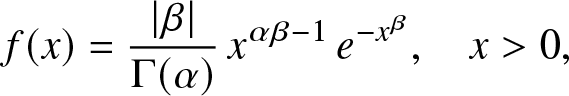 \begin{eqnarray*}
f(x)=\frac{\vert \beta\vert}{\Gamma(\alpha)}\, x^{\alpha\beta-1}\,e^{-x^{\beta}},\quad x \gt 0,
\end{eqnarray*}
\begin{eqnarray*}
f(x)=\frac{\vert \beta\vert}{\Gamma(\alpha)}\, x^{\alpha\beta-1}\,e^{-x^{\beta}},\quad x \gt 0,
\end{eqnarray*} where α > 0 and β ≠ 0 are shape parameters; see [Reference Johnson, Kotz and Balakrishnan11]. This means that  $X\stackrel{d}{=} {{\boldsymbol{\Gamma}}}_\alpha^{1/\beta}$, where
$X\stackrel{d}{=} {{\boldsymbol{\Gamma}}}_\alpha^{1/\beta}$, where ![]() ${{\boldsymbol{\Gamma}}}_\alpha$ is a standard gamma random variable with parameter
${{\boldsymbol{\Gamma}}}_\alpha$ is a standard gamma random variable with parameter ![]() $\alpha.$ We then have:
$\alpha.$ We then have:
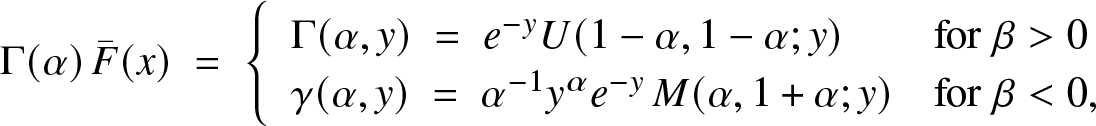 \begin{equation*}{\Gamma}(\alpha)\,{\bar F}(x) \; =\; \left\{\begin{array}{ll} \Gamma (\alpha, y)\; = \; e^{-y} U(1-\alpha, 1-\alpha; y) & \mbox{for}\ \beta \gt 0\\
\gamma (\alpha, y)\; = \; \alpha^{-1} y^\alpha e^{-y}\, M(\alpha, 1+\alpha; y) & \mbox{for}\ \beta \lt 0,\end{array}\right.\end{equation*}
\begin{equation*}{\Gamma}(\alpha)\,{\bar F}(x) \; =\; \left\{\begin{array}{ll} \Gamma (\alpha, y)\; = \; e^{-y} U(1-\alpha, 1-\alpha; y) & \mbox{for}\ \beta \gt 0\\
\gamma (\alpha, y)\; = \; \alpha^{-1} y^\alpha e^{-y}\, M(\alpha, 1+\alpha; y) & \mbox{for}\ \beta \lt 0,\end{array}\right.\end{equation*} with ![]() $y = x^\beta$ and the standard notation for incomplete gamma and confluent hypergeometric functions, see (5.6) and (5.6) in [Reference Slater20]. It is easy to check that
$y = x^\beta$ and the standard notation for incomplete gamma and confluent hypergeometric functions, see (5.6) and (5.6) in [Reference Slater20]. It is easy to check that ![]() $x\mapsto f(e^x)$ is always log-concave, and so is
$x\mapsto f(e^x)$ is always log-concave, and so is ![]() ${\bar F}(e^x)$ by Corollary 2.3. Based on hypergeometric functions, this can also be observed from
${\bar F}(e^x)$ by Corollary 2.3. Based on hypergeometric functions, this can also be observed from ![]() $xh(x) = \beta y^\alpha\!/U(1-\alpha,1-\alpha, y)$ for β > 0, with:
$xh(x) = \beta y^\alpha\!/U(1-\alpha,1-\alpha, y)$ for β > 0, with:
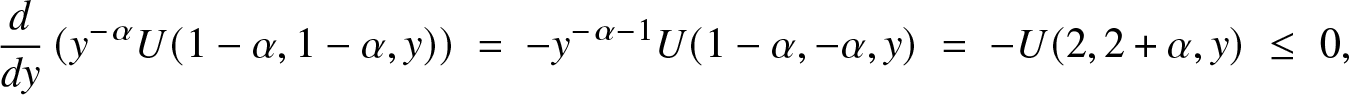 \begin{equation*}\frac{d}{dy}\left( y^{-\alpha} U(1-\alpha,1-\alpha, y)\right)\; =\; - y^{-\alpha -1} U(1-\alpha,-\alpha,y) \; = \; -U(2,2+\alpha, y)\; \le\; 0,\end{equation*}
\begin{equation*}\frac{d}{dy}\left( y^{-\alpha} U(1-\alpha,1-\alpha, y)\right)\; =\; - y^{-\alpha -1} U(1-\alpha,-\alpha,y) \; = \; -U(2,2+\alpha, y)\; \le\; 0,\end{equation*} by (2.1) and (1.4) in [Reference Slater20], and from ![]() $xh(x) = \alpha\beta/M(\alpha,1+\alpha, y)$ for
$xh(x) = \alpha\beta/M(\alpha,1+\alpha, y)$ for ![]() $\beta \lt 0,$ which is decreasing in y and hence increasing in
$\beta \lt 0,$ which is decreasing in y and hence increasing in ![]() $x,$ by positivity of the coefficients in the series defining
$x,$ by positivity of the coefficients in the series defining ![]() $M.$
$M.$
As far as the log-concavity of ![]() ${\bar F}$ is concerned, the situation depends on the sign of
${\bar F}$ is concerned, the situation depends on the sign of ![]() $\beta.$ For β < 0, we have
$\beta.$ For β < 0, we have ![]() $h(x) = y^{-1/\beta}\!/M(1,1+\alpha, y)\to 0$ as x → 0 and
$h(x) = y^{-1/\beta}\!/M(1,1+\alpha, y)\to 0$ as x → 0 and ![]() $x\to\infty,$ so that h is never monotone and neither
$x\to\infty,$ so that h is never monotone and neither ![]() ${\bar F}$ nor f are log-concave; on the other hand, when β > 0, we have
${\bar F}$ nor f are log-concave; on the other hand, when β > 0, we have ![]() $h(x) = \beta y^{\alpha-1/\beta}\!/U(1-\alpha,1-\alpha, y)$ and,
$h(x) = \beta y^{\alpha-1/\beta}\!/U(1-\alpha,1-\alpha, y)$ and,
The first equivalence is direct, and the inclusion in the second equivalence follows from Corollary 2.3. For the second reverse inclusion, we first observe again from (2.1) and (1.4) in [Reference Slater20] that:
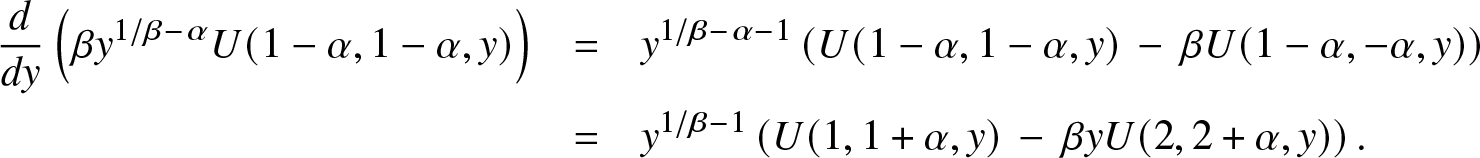 \begin{eqnarray*}
\frac{d}{dy}\left( \beta y^{1/\beta -\alpha} U(1-\alpha,1-\alpha, y)\right) & = & y^{1/\beta -\alpha-1}\left( U(1-\alpha,1-\alpha,y)\, - \, \beta U(1-\alpha,-\alpha, y)\right)\\
& = & y^{1/\beta -1}\left( U(1,1+\alpha,y)\, - \, \beta y U(2,2+\alpha, y)\right).
\end{eqnarray*}
\begin{eqnarray*}
\frac{d}{dy}\left( \beta y^{1/\beta -\alpha} U(1-\alpha,1-\alpha, y)\right) & = & y^{1/\beta -\alpha-1}\left( U(1-\alpha,1-\alpha,y)\, - \, \beta U(1-\alpha,-\alpha, y)\right)\\
& = & y^{1/\beta -1}\left( U(1,1+\alpha,y)\, - \, \beta y U(2,2+\alpha, y)\right).
\end{eqnarray*} From (3.1) in [Reference Slater20], the first quantity behaves like ![]() ${\Gamma}(\alpha)(1 -\alpha\beta) y^{1/\beta -\alpha-1} \gt 0$ as y → 0 when
${\Gamma}(\alpha)(1 -\alpha\beta) y^{1/\beta -\alpha-1} \gt 0$ as y → 0 when ![]() $\beta \ge 1$ and
$\beta \ge 1$ and ![]() $\alpha\beta \lt 1,$ while the second quantity behaves like
$\alpha\beta \lt 1,$ while the second quantity behaves like ![]() $(1 -\beta) y^{1/\beta -2} \gt 0$ as
$(1 -\beta) y^{1/\beta -2} \gt 0$ as ![]() $y\to \infty$ when β < 1. This shows that h has increase points on
$y\to \infty$ when β < 1. This shows that h has increase points on ![]() $(0,\infty)$ if
$(0,\infty)$ if ![]() $\inf\{\beta, \alpha\beta\} \lt 1.$ Notice that by using the same argument, we can show that:
$\inf\{\beta, \alpha\beta\} \lt 1.$ Notice that by using the same argument, we can show that:
for every β > 0.
The following example demonstrates a situation wherein the statement of Proposition 3.1 may not be an equivalence.
Example 3.3. Suppose X has a generalized beta distribution of the first kind with density:
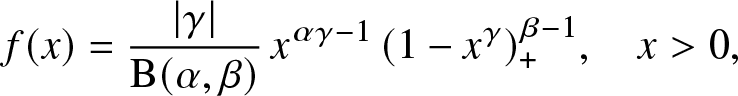 \begin{eqnarray*}
f(x)=\frac{\vert \gamma\vert}{{\rm B}(\alpha, \beta)}\, x^{\alpha\gamma-1}\, (1-x^\gamma)_+^{\beta-1},\quad x \gt 0,
\end{eqnarray*}
\begin{eqnarray*}
f(x)=\frac{\vert \gamma\vert}{{\rm B}(\alpha, \beta)}\, x^{\alpha\gamma-1}\, (1-x^\gamma)_+^{\beta-1},\quad x \gt 0,
\end{eqnarray*} with ![]() $\alpha, \beta \gt 0$ and γ ≠ 0. This means that
$\alpha, \beta \gt 0$ and γ ≠ 0. This means that  $X\stackrel{d}{=} {\bf B}_{\alpha,\beta}^{1/\gamma}$, where
$X\stackrel{d}{=} {\bf B}_{\alpha,\beta}^{1/\gamma}$, where ![]() ${\bf B}_{\alpha,\beta}$ is a standard Beta random variable with parameters
${\bf B}_{\alpha,\beta}$ is a standard Beta random variable with parameters ![]() $\alpha, \beta.$ Notice that when
$\alpha, \beta.$ Notice that when ![]() $\alpha = 1,$ we get the so-called Kumaraswamy distribution with parameters
$\alpha = 1,$ we get the so-called Kumaraswamy distribution with parameters ![]() $(\gamma,\beta)$ (see [Reference Kumaraswamy13]). Then, we have:
$(\gamma,\beta)$ (see [Reference Kumaraswamy13]). Then, we have:
 \begin{equation*}{\rm B}(\alpha,\beta) {\bar F}(x) \; =\; \left\{\begin{array}{ll} {\rm B} (1-y; \beta, \alpha)\; = \; \beta^{-1}(1-y)^\beta \,{}_2 F_{1}(1-\alpha, \beta, \beta+1, 1-y) & \mbox{for}\, \gamma \gt 0\\
{\rm B} (y; \alpha, \beta)\; = \; \alpha^{-1}y^\alpha \,{}_2 F_{1}(1-\beta, \alpha, \alpha+1; y)& \mbox{for}\, \gamma \lt 0,\end{array}\right.\end{equation*}
\begin{equation*}{\rm B}(\alpha,\beta) {\bar F}(x) \; =\; \left\{\begin{array}{ll} {\rm B} (1-y; \beta, \alpha)\; = \; \beta^{-1}(1-y)^\beta \,{}_2 F_{1}(1-\alpha, \beta, \beta+1, 1-y) & \mbox{for}\, \gamma \gt 0\\
{\rm B} (y; \alpha, \beta)\; = \; \alpha^{-1}y^\alpha \,{}_2 F_{1}(1-\beta, \alpha, \alpha+1; y)& \mbox{for}\, \gamma \lt 0,\end{array}\right.\end{equation*} with ![]() $y = x^\gamma\in (0,1)$ and the standard notation for the incomplete beta function and the Gaussian hypergeometric function. It is easy to check that:
$y = x^\gamma\in (0,1)$ and the standard notation for the incomplete beta function and the Gaussian hypergeometric function. It is easy to check that:
On the other hand, for γ > 0, Kummer’s transformation on ![]() ${}_2 F_{1}$ implies:
${}_2 F_{1}$ implies:
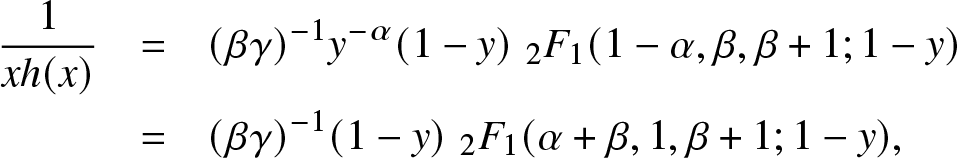 \begin{eqnarray*}
\frac{1}{xh(x)} & = & (\beta\gamma)^{-1} y^{-\alpha} (1-y)\, \,{}_2 F_{1}(1-\alpha, \beta, \beta+1; 1-y)\\
& = & (\beta\gamma)^{-1} (1-y)\, \,{}_2 F_{1}(\alpha+\beta, 1,\beta+1; 1-y),
\end{eqnarray*}
\begin{eqnarray*}
\frac{1}{xh(x)} & = & (\beta\gamma)^{-1} y^{-\alpha} (1-y)\, \,{}_2 F_{1}(1-\alpha, \beta, \beta+1; 1-y)\\
& = & (\beta\gamma)^{-1} (1-y)\, \,{}_2 F_{1}(\alpha+\beta, 1,\beta+1; 1-y),
\end{eqnarray*} which is a decreasing function in ![]() $x\in (0,1)$ by positivity of the coefficients in the series representation of
$x\in (0,1)$ by positivity of the coefficients in the series representation of ![]() ${}_2 F_{1}(\alpha+\beta, 1,\beta+1; 1-y).$ This shows that
${}_2 F_{1}(\alpha+\beta, 1,\beta+1; 1-y).$ This shows that ![]() $x\mapsto {\bar F}(e^x)$ is log-concave for all
$x\mapsto {\bar F}(e^x)$ is log-concave for all ![]() $\alpha,\beta,\gamma \gt 0.$
$\alpha,\beta,\gamma \gt 0.$
But, for γ < 0, the same hypergeometric transformation leads to:
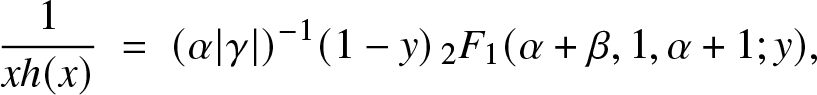 \begin{equation*}\frac{1}{xh(x)} \; = \; (\alpha\vert\gamma\vert)^{-1} (1-y)\, {}_2 F_{1}(\alpha+\beta, 1,\alpha+1; y),\end{equation*}
\begin{equation*}\frac{1}{xh(x)} \; = \; (\alpha\vert\gamma\vert)^{-1} (1-y)\, {}_2 F_{1}(\alpha+\beta, 1,\alpha+1; y),\end{equation*} which can be shown to be decreasing in ![]() $x\in (1,\infty)$ for β > 1 and increasing in
$x\in (1,\infty)$ for β > 1 and increasing in ![]() $x\in (1,\infty)$ for β < 1. This implies that either
$x\in (1,\infty)$ for β < 1. This implies that either ![]() $\beta \ge 1$ and
$\beta \ge 1$ and ![]() $x\mapsto f(e^x)$ and
$x\mapsto f(e^x)$ and ![]() $x\mapsto {\bar F}(e^x)$ are log-concave, or
$x\mapsto {\bar F}(e^x)$ are log-concave, or ![]() $\beta \le 1$ and
$\beta \le 1$ and ![]() $x\mapsto f(e^x)$ and
$x\mapsto f(e^x)$ and ![]() $x\mapsto {\bar F}(e^x)$ are log-convex. In particular, the statement of Proposition 3.1 is again an equivalence for γ < 0. It can also be shown that neither f nor
$x\mapsto {\bar F}(e^x)$ are log-convex. In particular, the statement of Proposition 3.1 is again an equivalence for γ < 0. It can also be shown that neither f nor ![]() ${\bar F}$ are log-concave for
${\bar F}$ are log-concave for ![]() $\gamma \lt 0,$ while
$\gamma \lt 0,$ while
for γ > 0.
If we consider β < 1 and γ > 0 in the above example, it is of interest to notice that ![]() $x\mapsto f(e^x)$ is log-convex on
$x\mapsto f(e^x)$ is log-convex on ![]() ${\mathbb{R}}^-$ while
${\mathbb{R}}^-$ while ![]() $x\mapsto {\bar F}(e^x)$ is log-concave on
$x\mapsto {\bar F}(e^x)$ is log-concave on ![]() ${\mathbb{R}}.$ From Remark 2.2 (c) and Corollary 2.3, this implies:
${\mathbb{R}}.$ From Remark 2.2 (c) and Corollary 2.3, this implies:
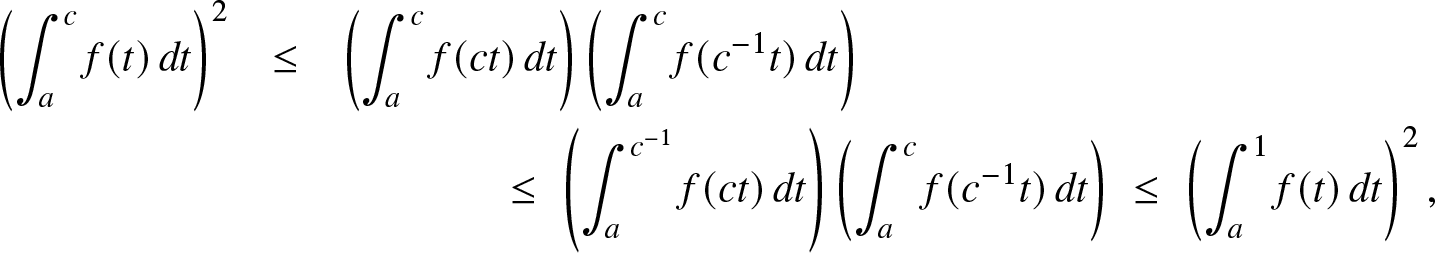 \begin{eqnarray*}
\left( \int_a^c f(t)\, dt\right)^2 & \le & \left(\int_a^c f(ct)\, dt\right)\left( \int_a^c f(c^{-1}t)\, dt\right)\\
& & \qquad\qquad\le\; \left(\int_a^{c^{-1}} f(ct)\, dt\right)\left( \int_a^c f(c^{-1} t)\, dt\right)\; \le\; \left( \int_a^1 f(t)\, dt\right)^2,
\end{eqnarray*}
\begin{eqnarray*}
\left( \int_a^c f(t)\, dt\right)^2 & \le & \left(\int_a^c f(ct)\, dt\right)\left( \int_a^c f(c^{-1}t)\, dt\right)\\
& & \qquad\qquad\le\; \left(\int_a^{c^{-1}} f(ct)\, dt\right)\left( \int_a^c f(c^{-1} t)\, dt\right)\; \le\; \left( \int_a^1 f(t)\, dt\right)^2,
\end{eqnarray*} for all a < c in ![]() $(0,1).$ We refer to [Reference An3] for further discussions on the asymmetry between log-concavity and log-convexity in a probabilistic framework. One may also refer to [Reference Hansen9] for a characterization based on Lévy measures, in the framework of infinitely divisible distributions.
$(0,1).$ We refer to [Reference An3] for further discussions on the asymmetry between log-concavity and log-convexity in a probabilistic framework. One may also refer to [Reference Hansen9] for a characterization based on Lévy measures, in the framework of infinitely divisible distributions.
3.2. On failure rates of  $(n-k+1)$-out-of-n systems with discrete lifetimes
$(n-k+1)$-out-of-n systems with discrete lifetimes
Let Z be a random variable with support ![]() $S_Z\subseteq {\mathbb{N}}$,
$S_Z\subseteq {\mathbb{N}}$, ![]() $p_i={\mathbb{P}}[Z=i]$ be its probability mass function (pmf),
$p_i={\mathbb{P}}[Z=i]$ be its probability mass function (pmf), ![]() $F_i={\mathbb{P}}[Z\le i]$ be its cumulative distribution function (cdf), and
$F_i={\mathbb{P}}[Z\le i]$ be its cumulative distribution function (cdf), and ![]() $\bar{F}_i=P[Z \gt i]$ be its survival function (sf). The failure rate of this distribution has been defined as (see [Reference Johnson, Kemp and Kotz10] p.45):
$\bar{F}_i=P[Z \gt i]$ be its survival function (sf). The failure rate of this distribution has been defined as (see [Reference Johnson, Kemp and Kotz10] p.45):
 \begin{equation*}h(i)\;=\;\frac{{\mathbb{P}}[Z=i]}{{\mathbb{P}}[Z \geq i]}\;=\;\frac{p_i}{\bar{F}_{i-1}}\;=\;1\,-\,\frac{\bar{F}_i}{\bar{F}_{i-1}},\end{equation*}
\begin{equation*}h(i)\;=\;\frac{{\mathbb{P}}[Z=i]}{{\mathbb{P}}[Z \geq i]}\;=\;\frac{p_i}{\bar{F}_{i-1}}\;=\;1\,-\,\frac{\bar{F}_i}{\bar{F}_{i-1}},\end{equation*} for all ![]() $i \in S_Z.$ Z is said to have the IFR property if its failure rate is non-decreasing. From the above, it means that
$i \in S_Z.$ Z is said to have the IFR property if its failure rate is non-decreasing. From the above, it means that ![]() $i\mapsto \bar{F}_{i}/\bar{F}_{i-1}$ is non-increasing, or equivalently,
$i\mapsto \bar{F}_{i}/\bar{F}_{i-1}$ is non-increasing, or equivalently, ![]() $\{\bar{F}_{i}\}$ is a logconcave sequence, i.e.,
$\{\bar{F}_{i}\}$ is a logconcave sequence, i.e.,
for all ![]() $i\ge 0.$ Let
$i\ge 0.$ Let ![]() $Z_1,\dots,Z_n$ be n independent copies of Z and
$Z_1,\dots,Z_n$ be n independent copies of Z and ![]() $Z_{k:n}$ be the k-th order statistic, for
$Z_{k:n}$ be the k-th order statistic, for ![]() $1\leq k \leq n.$ This is the same as the lifetime of an
$1\leq k \leq n.$ This is the same as the lifetime of an ![]() $(n-k+1)$-out-of-n system; see [Reference Barlow and Proschan5], for example (some properties on ageing notions and order statistics in the discrete case can be found in [Reference Alimohammadi, Alamatsaz and Cramer1] and the references therein). The following theorem presents an alternative proof to the main result of [Reference Alimohammadi and Navarro2] which states that the IFR property is preserved by order statistics. A continuous version of this result had been established about six decades ago by Esary and Proschan [Reference Esary and Proschan8].
$(n-k+1)$-out-of-n system; see [Reference Barlow and Proschan5], for example (some properties on ageing notions and order statistics in the discrete case can be found in [Reference Alimohammadi, Alamatsaz and Cramer1] and the references therein). The following theorem presents an alternative proof to the main result of [Reference Alimohammadi and Navarro2] which states that the IFR property is preserved by order statistics. A continuous version of this result had been established about six decades ago by Esary and Proschan [Reference Esary and Proschan8].
Theorem 3.4. If Z has IFR property, then ![]() $Z_{k:n}$ has IFR property for all
$Z_{k:n}$ has IFR property for all ![]() $n\ge 1$ and
$n\ge 1$ and ![]() $1\le k\le n.$
$1\le k\le n.$
Proof. Setting  $p_i^{k:n}, F_i^{k:n}$ and
$p_i^{k:n}, F_i^{k:n}$ and  $\bar{F}_i^{k:n}$ for the respective pmf, cdf and sf of
$\bar{F}_i^{k:n}$ for the respective pmf, cdf and sf of ![]() $Z_{k:n},$ we start with the expression:
$Z_{k:n},$ we start with the expression:
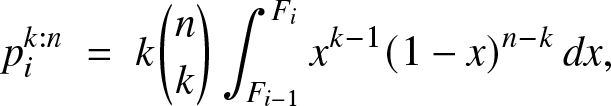 \begin{equation*}
p_i^{k:n}\;=\; k\binom {n}{k}\int_{F_{i-1}}^{F_{i}}x^{k-1}(1-x)^{n-k}\,dx,\end{equation*}
\begin{equation*}
p_i^{k:n}\;=\; k\binom {n}{k}\int_{F_{i-1}}^{F_{i}}x^{k-1}(1-x)^{n-k}\,dx,\end{equation*}given in [Reference Arnold, Balakrishnan and Nagaraja4] p. 42, for example. This implies
 \begin{equation*}\bar{F}_i^{k:n}\; =\;\sum_{j=i+1}^{\infty}p_j^{k:n}= k\binom{n}{k}\int_{F_{i}}^{1}x^{k-1}(1-x)^{n-k}\,dx\; =\; \int_{0}^{\bar{F}_i}f_{k:n}(x)\, dx,\end{equation*}
\begin{equation*}\bar{F}_i^{k:n}\; =\;\sum_{j=i+1}^{\infty}p_j^{k:n}= k\binom{n}{k}\int_{F_{i}}^{1}x^{k-1}(1-x)^{n-k}\,dx\; =\; \int_{0}^{\bar{F}_i}f_{k:n}(x)\, dx,\end{equation*}with the notation:
 \begin{equation*}f_{k:n}(x)\;=\;k\binom{n}{k}\, x^{n-k}(1-x)^{k-1},\end{equation*}
\begin{equation*}f_{k:n}(x)\;=\;k\binom{n}{k}\, x^{n-k}(1-x)^{k-1},\end{equation*} which is easily seen to be such that ![]() $f_{k:n}(e^x)$ is log-concave function for all
$f_{k:n}(e^x)$ is log-concave function for all ![]() $n\ge 1$ and
$n\ge 1$ and ![]() $1\le k\le n.$ Applying now Corollary 2.3 with a = 0,
$1\le k\le n.$ Applying now Corollary 2.3 with a = 0, ![]() $b=\bar{F}_i$ and
$b=\bar{F}_i$ and ![]() $c = \bar{F}_{i-1}/\bar{F}_i,$ we obtain:
$c = \bar{F}_{i-1}/\bar{F}_i,$ we obtain:
 \begin{eqnarray*}
(\bar{F}_i^{k:n})^2\;= \; \left( \int_{0}^{\bar{F}_i}f_{k:n}(x)\, dx\right)^2 &\geq & \left( \int_{0}^{\bar{F}_i} f_{k:n}(cx)\, dx\right)\!\left( \int_{0}^{\bar{F}_i} f_{k:n}(c^{-1} x)\, dx\right) \\
&= & \!\!\left( \int_{0}^{(\bar{F}_i)^2/\bar{F}_{i-1}} f_{k:n}(x)\, dx\right)\!\left( \int_{0}^{\bar{F}_{i-1}} f_{k:n}(x)\, dx\right)\\
&\ge &\!\! \left( \int_{0}^{\bar{F}_{i+1}} f_{k:n}(x)\, dx\right)\!\left( \int_{0}^{\bar{F}_{i-1}} f_{k:n}(x)\, dx\right)\, =\,\bar{F}_{i-1}^{k:n} \bar{F}_{i+1}^{k:n},
\end{eqnarray*}
\begin{eqnarray*}
(\bar{F}_i^{k:n})^2\;= \; \left( \int_{0}^{\bar{F}_i}f_{k:n}(x)\, dx\right)^2 &\geq & \left( \int_{0}^{\bar{F}_i} f_{k:n}(cx)\, dx\right)\!\left( \int_{0}^{\bar{F}_i} f_{k:n}(c^{-1} x)\, dx\right) \\
&= & \!\!\left( \int_{0}^{(\bar{F}_i)^2/\bar{F}_{i-1}} f_{k:n}(x)\, dx\right)\!\left( \int_{0}^{\bar{F}_{i-1}} f_{k:n}(x)\, dx\right)\\
&\ge &\!\! \left( \int_{0}^{\bar{F}_{i+1}} f_{k:n}(x)\, dx\right)\!\left( \int_{0}^{\bar{F}_{i-1}} f_{k:n}(x)\, dx\right)\, =\,\bar{F}_{i-1}^{k:n} \bar{F}_{i+1}^{k:n},
\end{eqnarray*} where for the second inequality we have used ![]() $(\bar{F}_i)^2\geq \bar{F}_{i-1}\bar{F}_{i+1}$ comes from the IFR property of Z. Hence, the theorem.
$(\bar{F}_i)^2\geq \bar{F}_{i-1}\bar{F}_{i+1}$ comes from the IFR property of Z. Hence, the theorem.
The above method also allows us to obtain the stability result for the reversed failure rate of the discrete random variable Z. With the notation as above, the reversed failure rate is defined as:
 \begin{equation*}r(i)\;=\;\frac{{\mathbb{P}}[Z=i]}{{\mathbb{P}}[Z \leq i]}\;=\;\frac{p_i}{F_i}\;=\;1\,-\,\frac{F_{i-1}}{F_i}.\end{equation*}
\begin{equation*}r(i)\;=\;\frac{{\mathbb{P}}[Z=i]}{{\mathbb{P}}[Z \leq i]}\;=\;\frac{p_i}{F_i}\;=\;1\,-\,\frac{F_{i-1}}{F_i}.\end{equation*} Then, Z is said to have the DRFR property if r(i) is non-increasing in i, which means that ![]() $\{{F}_i\}$ is a log-concave sequence. The following is a discrete counterpart to a result in Theorem 2.1 of Kundu, Nanda and Hu [Reference Kundu, Nanda and Hu14].
$\{{F}_i\}$ is a log-concave sequence. The following is a discrete counterpart to a result in Theorem 2.1 of Kundu, Nanda and Hu [Reference Kundu, Nanda and Hu14].
Theorem 3.5. If Z has DRFR property, then ![]() $Z_{k:n}$ has DRFR property for all
$Z_{k:n}$ has DRFR property for all ![]() $n\ge 1$ and
$n\ge 1$ and ![]() $1\le k\le n.$
$1\le k\le n.$
Proof. Let us consider the expresion:
 \begin{equation*}{F}_i^{k:n}\; =\; \int_{0}^{F_i}g_{k:n}(x)\,dx,\end{equation*}
\begin{equation*}{F}_i^{k:n}\; =\; \int_{0}^{F_i}g_{k:n}(x)\,dx,\end{equation*}for the cdf of kth order statistic, with the notation:
 \begin{equation*}g_{k:n}(x)\;=\;f_{k:n}(1-x)\;=\;k\binom{n}{k}\, x^{k-1}(1-x)^{n-k}.\end{equation*}
\begin{equation*}g_{k:n}(x)\;=\;f_{k:n}(1-x)\;=\;k\binom{n}{k}\, x^{k-1}(1-x)^{n-k}.\end{equation*} It is evident that ![]() $f_{k:n}(e^x)$ is a log-concave function for all
$f_{k:n}(e^x)$ is a log-concave function for all ![]() $n\ge 1$ and
$n\ge 1$ and ![]() $1\le k\le n.$ The proof of this theorem then proceeds along the same lines as that of Theorem 3.4, using the inequality
$1\le k\le n.$ The proof of this theorem then proceeds along the same lines as that of Theorem 3.4, using the inequality ![]() $({F}_i)^2\geq{F}_{i-1} {F}_{i+1}$.
$({F}_i)^2\geq{F}_{i-1} {F}_{i+1}$.
Remark 3.6. The following example shows that the converse results of Theorems 3.4 and 3.5 are not true in general. Suppose ![]() ${\mathbb{P}} [Z=1] ={\mathbb{P}}[Z=3] = 2/5$ and
${\mathbb{P}} [Z=1] ={\mathbb{P}}[Z=3] = 2/5$ and ![]() ${\mathbb{P}}[Z=2] = 1/5.$ Then, we find that
${\mathbb{P}}[Z=2] = 1/5.$ Then, we find that ![]() $h(1) = r(3) = 2/5, h(2) = r(2) = 1/3$ and
$h(1) = r(3) = 2/5, h(2) = r(2) = 1/3$ and ![]() $h(3) = r(1) = 1$, so that h and r are not monotone. On the other hand, we have:
$h(3) = r(1) = 1$, so that h and r are not monotone. On the other hand, we have:
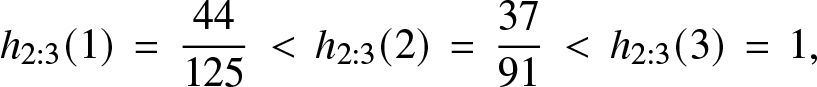 \begin{equation*}h_{2:3}(1) \, =\, \frac{44}{125}\, \lt \,h_{2:3}(2) \, =\, \frac{37}{91}\, \lt \, h_{2:3}(3) \, =\, 1,\end{equation*}
\begin{equation*}h_{2:3}(1) \, =\, \frac{44}{125}\, \lt \,h_{2:3}(2) \, =\, \frac{37}{91}\, \lt \, h_{2:3}(3) \, =\, 1,\end{equation*} and so ![]() $Z_{2:3}$ is IFR; similarly
$Z_{2:3}$ is IFR; similarly
 \begin{equation*}r_{1:3}(3) \, =\, \frac{8}{125}\, \lt \,r_{1:3}(2) \, =\, \frac{19}{117}\, \lt \, r_{1:3}(1) \, =\, 1,\end{equation*}
\begin{equation*}r_{1:3}(3) \, =\, \frac{8}{125}\, \lt \,r_{1:3}(2) \, =\, \frac{19}{117}\, \lt \, r_{1:3}(1) \, =\, 1,\end{equation*} and so ![]() $Z_{1:3}$ is DRFR.
$Z_{1:3}$ is DRFR.
Acknowledgments
We express our sincere thanks to the anonymous reviewer and the Editor-in-Chief for their incisive comments on an earlier version of this manuscript which led to this improved version.


