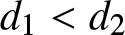Analyzing the multi-state system under a run shock model

Abstract

A system experiences random shocks over time, with two critical levels, d₁ and d₂, where $d_{1} \lt d_{2}$. k consecutive shocks with magnitudes between d₁ and d₂ partially damaging the system, causing it to transition to a lower, partially working state. Shocks with magnitudes above d₂ have a catastrophic effect, resulting in complete failure. This theoretical framework gives rise to a multi-state system characterized by an indeterminate quantity of states. When the time between successive shocks follows a phase-type distribution, a detailed analysis of the system’s dynamic reliability properties such as the lifetime of the system, the time it spends in perfect functioning, as well as the total time it spends in partially working states are discussed.

1. Introduction

The time interval between consecutive shocks or the shock-induced damage usually defines system failure in shock models. Various shock models have been proposed and examined in the literature, which can be categorized into five groups: extreme shock model [2, 6], run shock model [19, 22], δ-shock model [14, 15], cumulative shock model [8, 26], and mixed shock model [9, 27]. The mixed shock model combines at least two different shock models. In [7], for instance, system fails upon the occurrence of k ₁ consecutive shocks of size between d ₁ and d ₂ or a single large shock of size at least d ₂. Recently, Ozkut [21] extended this model by combining two run shock models. One can see other mixed shock models in [11, 20].

The extreme shock model states that a system will fail if an individual shock surpasses a certain level, denoted by d [24]. The time between shocks is represented by T_i, while the magnitude of the shock is represented by Y_i. The lifetime of the system, S, is calculated as S = $\sum\limits_{i=1}^{N}T_{i}$, with the stopping random variable N defined as $\left\{N=n\right\} \equiv\left\{Y_{1}\leq d,\ldots,Y_{n-1}\leq d,Y_{n} \gt d\right\} $. This model has been explored in several studies [4, 10, 28].

Particularly in contemporary real-world scenarios, it is imperative to take into account the extensive array of potential system states. Furthermore, the escalating requisites for system assessment and design pose challenges to the applicability of conventional binary systems. The conceptualization of multi-state systems was initially propounded by the work of [13] in the year 1968. Subsequent to this seminal contribution, investigations into the realm of multi-state systems have been ongoing in fields, such as reliability theory, strategic decision theory, and health-care [1, 16, 17].

Many researchers pay much more attention to the shock models in binary settings, but there are very few studies on their extensions to multi-state systems [5, 29]. Zhao et al. [29] classified shocks into three types , such as the highest, medium and the lowest impact on the system, according to the severity of the impact of the shock event on the environment. Eryilmaz [5] presented an extreme shock model in which a large shock causes complete failure, as in the classical model, for a multi-state system. In such a shock model, the system fails when a shock with large magnitude occurs. If the magnitude of a shock is between two critical levels, it has partial damage and leads the system to a lower state. although the working state gets lower and lower, the system never breaks down, no matter how many shocks with partial damage occur before a large shock. In many real life incidence transitions to lower state occurs due to occurrence of k consecutive shocks which is a more general form of the precedence. More precisely, if k consecutive shocks’ magnitude fall between two critical levels d ₁ and d ₂, ($d_{1} \lt d_{2}),$ the system transitions to a partially working state with reduced capacity. Therefore, the present paper generalizes the extreme shock models given in [5] to run shock models in multi-state systems. That is, the proposed model becomes extreme shock model when k = 1. The new extension is more flexible. Consequently, we will able to model more real life situations. In credit risk modeling, shocks can be related to economical events such as crisis and recessions [18], in network modeling, they can be cyber attacks like distributed denial of service (DDoS) [25], and in insurance, they are natural disasters or accidents. For example, an insurance companies updates credit scores (states) of their customers after random accidents (shocks). Each accident has different costs (shock magnitude). Consecutive accidents having costs between thresholds d ₁ and d ₂ will lead to a change in the customers’ credit scores. But the customer still continues to benefit from advantages of the insurance. If a catastrophic accident which costs more than d ₂ occurs, then customer will no longer get insured. The structure of this paper has been designed in the following way: the system design is outlined in Section 2, while a detailed analysis of the system’s dynamic reliability properties is provided in Section 3. Finally, a numerical illustration is given in Section 4.

2. System design

Suppose there are two critical levels, d ₁ and d ₂, with d ₁ $ \lt d_{2}$. If k consecutive shocks $(k\geq1)$ with a magnitude between these levels, they will partially damage the system and put it into a lower, partially functional state. Each additional k consecutive shocks in this range further reduces the state of the system by one unit. However, if a shock of larger than d ₂, it will have a devastating effect and result in complete failure. The number of states of the system is random, represented by $\Psi(s)$ at time s, where $\Psi(s)$ $\in$ $\left\{0,1,\ldots,N_{v}^{(k)}+1\right\}$. Let $N_{v}^{(k)}$ be a random variable denoting the number of k consecutive shocks, whose magnitude is between d ₁ and d ₂ until the first extreme shock above $d_{2},$ in a total number of shocks v. The states “$N_{v}^{(k)}+1"$ and “0” correspond to perfect functioning and complete failure, respectively, with a total of $N_{v}^{(k)}+1$ working states $\left\{1,\ldots,N_{v}^{(k)}+1\right\} $. At s = 0, the system works perfectly and will continue to do so until the first k successive shocks within $(d_{1},d_{2})$ or a shock above d ₂. Let S ^j be the amount of time that the system has spent in state $j,$ $j=1,\ldots,$ $N_{v}^{(k)}+1$. The length of time the system will operate at its best can also be represented by $S^{N_{v}^{(k)}+1},$ and the lifetime of the system is $S=S^{1}+\ldots+S^{N_{v}^{(k)}+1}$. Hence, for $N_{v}^{(k)}=0,$ $S^{N_{v}^{(k)}+1}$ is equal to the lifetime of the system, S. Clearly, $S-S^{N_{v}^{(k)}+1}$ is a random variable denoting the time elapsed following the first k successive shocks between critical levels d ₁ and d ₂ until the occurrence of the catastrophic shock. More precisely, $S-S^{N_{v}^{(k)}+1}$ is the time elapsed in partially working states. To gain a deeper insight into the model, a possible realization is presented in Figure 1.

Figure 1. A potential instance of the system and state variation processes.

According to Figure 1, for k = 2, the system is in the perfect state until the fourth shock occurs since Y ₃ and Y ₄ are the first two consecutive shocks between d ₁ and d ₂. After the fourth shock, the system transits into a lower state, and continues to function partially. Then Y ₇ and Y ₈ are the second two consecutive shocks between d ₁ and d ₂. After the eighth shock, the system transits into a lower state, and continues to function partially. Finally, a catastrophic shock Y ₁₁ causes the system failure. In this realization, there are totally two two-consecutive shocks until the system failure. Hence, $N_{11}^{(2)}=2$ and the system lifetime is $\displaystyle S=S^1+S^2+S^3$.

The proposed model can be used in urban planning, power transmission network, network reliability and information technology and cyber security. Security of the system is affected by DDoS attacks (shocks) which makes an online services unavailable to customers by temporarily or permanently cutting the host server. If the network cloud center is subject to consecutive attacks between critical volume levels d ₁ and d ₂, the cloud will leak information but still operate with a reduced trust index. A complete failure of the server occurs when the volume of the DDoS attack exceeds the volume level d ₂. The random variable $S^{N_{v}^{(k)}+1}$ represents the time that the server has worked with full trust.

2.1. Phase-type distribution

It is worth mentioning that phase-type distributions are useful in reliability evaluations of the systems since they provide a flexible and versatile framework to model complex failure patterns in systems. They are particularly valuable when analyzing systems with multiple phases of operation, such as start-up, steady-state, and shutdown, as well as when considering repair maintenance activities. They also enable the calculation of important reliability metrics such as mean time to failure, system lifetime and aiding in better decision making for system design, maintenance strategies and optimization.

The cumulative distribution function for a non-negative continuous phase-type random variable T is denoted by:

\begin{equation*} P\left( T\leq x\right) =1- \boldsymbol\zeta\mathbf{\exp}\left( \boldsymbol\Lambda\, x\right) \mathbf{e}^{\prime}, \end{equation*}

where the dimension of the non-singular matrix Λ is m × m. Furthermore, diagonal and non-diagonal elements are respectively negative and non-negative, and all row sums are non-positive. Additionally, the order of a substochastic vector ζ is m, and all elements are non-negative, and $ \boldsymbol\zeta\mathbf{e}^{\prime}\leq1$. We shall use $T\sim$ $PH_{c}\left( \boldsymbol\zeta,\boldsymbol\Lambda\right)$ to represent the continuous phase-type distribution. The expected value of T is given by:

\begin{equation*} E\left( T\right) =- \boldsymbol \zeta\boldsymbol\Lambda^{-1} \mathbf{e} ^{\prime}. \end{equation*}

On the other hand, the distribution of the time it takes for an absorbing Markov chain to reach an absorbing state is called a discrete phase-type distribution. The probability mass function (PMF) of a discrete random variable N which has a discrete phase-type distribution is represented by:

\begin{equation*} P\left( N=n\right) =\mathbf{a\boldsymbol\Psi}^{n-1}\mathbf{u}^{\prime}, \end{equation*}

for $n=1,2,\ldots$ and the matrix $\boldsymbol\Psi=\left( \psi_{ij}\right) _{m\times m}$ consists of the transition probabilities among the m transient states, the elements of the vector $~\mathbf{u}^{\prime}=\left( \mathbf{I}-\boldsymbol\Psi\right) \mathbf{e}^{\prime}$ are transition probabilities from transient states to the absorbing state, $\mathbf{a}=\left( a_{1},\ldots,a_{m}\right) $ with $ {\displaystyle\sum\limits_{i=1}^{m}} a_{i}=1,$ and I is the identity matrix. $N\sim$ $PH_{d}\left( \mathbf{a},\boldsymbol\Psi\right)$ will be used to represent the random variable N has a discrete phase-type distribution. The next propositions will be useful for the followings.

Proposition 1. Let $T_{1},T_{2},\ldots$ be independent and $T_{i}\sim PH_{c}\left( \boldsymbol\zeta,\boldsymbol\Lambda\right) ,$ and independently $N\sim PH_{d}\left(\mathbf{a},\boldsymbol\Psi\right) $. Then

\begin{equation*} S= {\displaystyle\sum\limits_{i=1}^{N}} T_{i}\sim PH_{c}\left( \boldsymbol\zeta\otimes\mathbf{a},\boldsymbol\Lambda \otimes\mathbf{I}+\left( \mathbf{a}^{0} \boldsymbol\zeta\right) \otimes \boldsymbol\Psi\right), \end{equation*}

where ⊗ is the Kronecker product [12].

Proposition 2. Suppose T is a continuous phase-type random variable represented by $T\sim PH_{c}\left( \boldsymbol\zeta,\boldsymbol\Lambda\right)$. Then, the distribution of $\left\{T-x|T \gt x\right\}$ can be expressed as $PH\left( \frac{\boldsymbol\zeta\exp\left( \boldsymbol\Lambda t\right) }{\boldsymbol\zeta\exp\left( \boldsymbol\Lambda t\right) e^{\prime}},\boldsymbol\Lambda\right)$ according to He [12]. As a result, the mean residual life (MRL) of T can be calculated from:

(1)\begin{equation} E\left( T-x|T \gt x\right) =-\frac{\boldsymbol\zeta\exp\left( \boldsymbol\Lambda t\right) }{\boldsymbol\zeta\exp\left( \boldsymbol\Lambda t\right) e^{\prime} }\boldsymbol\Lambda^{-1}\mathbf{e}^{\prime}. \end{equation}

3. System evaluation

Let $p_{1}=P(Y_{i}\leq d_{1}),$ $p_{2}=P(Y_{i}\ \in(d_{1},d_{2}))$ and $p_{3}=P(Y_{i} \gt d_{2})$ for $d_{1} \lt d_{2}$ and $i=1,2,\ldots$ We consider that inter-arrival times $T_{1},T_{2},\ldots$ and the magnitude of shocks $Y_{1},Y_{2},\ldots$ are independent.

Let V represent the number of shocks preceding the initial shock exceeding d ₂ occurs. Then,

\begin{equation*} P(V=v)=(1-p_{3})^{v-1}p_{3}, \end{equation*}

$v=1,2,\ldots$

Given that the random variable V follows a geometric distribution, Proposition 1 can be applied to show that the lifetime random variable $S=\sum\limits_{i=1}^{V}T_{i}$ exhibits a phase-type distribution with a corresponding survival function:

(2)\begin{equation} P\left( S \gt s\right) = \boldsymbol\zeta\exp\left( \left( \boldsymbol\Lambda+\left( 1-p_{3}\right) \boldsymbol\Lambda^{0} \boldsymbol\zeta\right) s\right) \mathbf{e} ^{\prime}. \end{equation}

Let the random variable $N_{v}^{(k)}$ represents the number of k consecutive shocks whose magnitude is between d ₁ and d ₂ until the occurrence of the first extreme shock over d ₂ in a total number of shocks v. Since the probability that a shock whose magnitude is above d ₂ given that it is greater than d ₁ is $\frac{p_{3}}{1-p_{1}},$ where $p_{3}=1-p_{1}-p_{2},$ then using Theorem 2.1 in [23],

\begin{align*} P\left( N_{v}^{(k)}=x\right) & =\left( \sum_{i=0}^{k-1}\sum_{x_{1} ,x_{2,\ldots,}x_{k}}\left( \begin{array} [c]{c} x_{1}+\cdots+x_{k}+x\\ x_{1},\cdots,x_{k},x, \end{array} \right) p^{v-1}\left( \frac{q}{p}\right) ^{x_{1}+\cdots+x_{k}}\right) \left( 1-p\right), \\ x & =0,1,\ldots,\left\lfloor \frac{v-1}{k}\right\rfloor, \end{align*}

where $p=\frac{p_{2}}{1-p_{1}}$ and $q=1-\frac{p_{2}}{1-p_{1}}$. In this equation, $x=0,1,\ldots, \left\lfloor \frac{v-1}{k}\right\rfloor$ are the possible states of the system, x = 0 indicates there is no k consecutive shocks in total v number of shocks while $x=\left\lfloor \frac{v-1}{k}\right\rfloor$ indicates the maximum number of k consecutive shocks in total v − 1 number of shocks since the last shock is always the catastrophic one.

In addition, $N_{v}^{(k)}+1$ denotes the number of functional states of the system with PMF:

\begin{align*} P\left( N_{v}^{(k)}+1=x\right) & =\left( \sum_{i=0}^{k-1}\sum _{x_{1},x_{2,\ldots,}x_{k}}\left( \begin{array} [c]{c} x_{1}+\cdots+x_{k}+x-1\\ x_{1},\cdots,x_{k},x-1 \end{array} \right) p^{v-1}\left( \frac{q}{p}\right) ^{x_{1}+\cdots+x_{k}}\right) \left( 1-p\right), \\ x & =1,\ldots,\left\lfloor \frac{v-1}{k}\right\rfloor+1, \end{align*}

where $p=\frac{p_{2}}{1-p_{1}}$ and $q=1-\frac{p_{2}}{1-p_{1}}$.

Let U ₁ be the number of shocks before the first k successive shocks whose magnitude is between d ₁ and d ₂ occur. Similarly, U_i is the number additional shocks to get the ith k consecutive shocks in $(d_{1},d_{2})$ after occurrence of the $(i-1)$th k consecutive shocks in $(d_{1},d_{2}),$ $i=2,\ldots,N_{v}^{(k)}$ and $U_{N_{v}^{(k)}+1}$ is the number of additional k consecutive shocks in $(d_{1},d_{2})$ to get the extreme shock whose magnitude is above d ₂.

Lemma 3. $u_{1}+\cdots+u_{x+1}=v,u_{1} \gt 0,\cdots,u_{x+1} \gt 0,$ $x=0,1,\ldots\left\lfloor \frac{v-1}{k}\right\rfloor $ and $v=1,2,\ldots$

\begin{equation*} P\left( U_{1}=u_{1},\ldots,U_{x+1}=u_{x+1},N_{v}^{(k)}=x,V=v\right) = {\displaystyle\prod\limits_{i=1}^{x+1}} P_{U_{i},k}, \end{equation*}

where

\begin{align*} & _{P_{U_{i},k}=\left\{ \begin{array} [c]{cc} {\displaystyle\sum\limits_{x_{2}=0}^{U_{i}-k-1}} N(x_{2},U_{i}-k-1,k)p_{2}^{x_{2}}p_{1}^{U_{i}-k-1-x_{2}}p_{1}p_{2}^{k} & ,\quad U_{i} \gt k\\ p_{2}^{k} & ,\quad U_{i}=k \end{array} \right. }\\ & \text{and}\\ & _{P_{U_{x+1},k}= {\displaystyle\sum\limits_{x_{2}=0}^{\min(U_{x+1}-1,k)}} N(x_{2},U_{x+1}-1-x_{2}+1,k)p_{2}^{x_{2}}p_{1}^{U_{x+1}-1-x_{2}}p_{3}} \end{align*}

$i=1,\ldots x,$ where

\begin{equation*} N(d,n,k)=\left\{ \begin{array} [c]{cc} \binom{n}{d} & \text{if }d \lt n\\ 0 & \text{if }n=d\geq k\\ {\displaystyle\sum\limits_{i=0}^{k-1}} N(d-i,n-1-i,k) & \text{if }n \gt d\geq k \end{array} \right. \end{equation*}

[3].

Corollary 4. The joint distribution of U ₁ and V is:

\begin{align*} & P\left( U_{1}=u,V=v\right) \\& \quad =\left\{\begin{aligned} {\displaystyle\sum\limits_{x_{2}=0}^{u-k-1-\left\lfloor \frac{u-k-1}{k}\right\rfloor}} N(x_{2},u-k-1,k)p_{1}^{u-k-x_{2}}(p_{1}+p_{2})^{v-1-u}p_{2}^{k+x_{2}}p_{3} & \quad if\ u \lt v\ and\ u\geq k\\ \left[{\displaystyle\sum\limits_{x_{12}=0}^{v-1-\left\lfloor \frac{v-1}{k}\right\rfloor }} N(x_{12},v-k-1,k)p_{1}^{v-1-x_{12}}p_{2}^{x_{12}}p_{3}\right] \times & \quad if\ u-v\geq k\\ \begin{array}{c} \left[{\displaystyle\sum\limits_{x_{22}=0}^{u-v-1-k-\left\lfloor \frac{u-v-1-k}{k}\right\rfloor }} N(x_{22},u-v-1-k,k)\left( p_{1}+p_{3}\right) p_{2}^{k+x_{22}}\times\right.\\ \left. {\displaystyle\sum\limits_{j=0}^{u-v-1-k-x_{22}}} \binom{u-v-1-k}{j\,}p_{1}^{j}p_{3}^{u-v-1-k-x_{22}-j}\right]\\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!0 \end{array} & \\ \quad otherwise \end{aligned} \right. \end{align*}

Corollary 5.

\begin{equation*} P(V \lt U_{1})= {\displaystyle\sum\limits_{v=1}} {\displaystyle\sum\limits_{u=v+1}} P(U_{1}=u,V=v) \end{equation*}

and

\begin{equation*} P(U_{1} \lt V)= {\displaystyle\sum\limits_{u=1}} {\displaystyle\sum\limits_{v=u+1}} P(U_{1}=u,V=v). \end{equation*}

Theorem 6. Let T_i denote the inter-arrival time between the $(i-1)$th and ith shocks, $i\geq2$. The survival function of $S^{N_{v}^{(k)}+1}$ can be calculated by:

(3)\begin{equation} P\left( S^{N_{v}^{(k)}+1} \gt s\right) =\left( \boldsymbol\zeta\otimes \mathbf{a}\right) \exp\left( \left( \boldsymbol\Lambda\otimes\mathbf{I}+\left( \mathbf{a}^{0} \boldsymbol\zeta\right) \otimes\boldsymbol\Psi\right) s\right) \mathbf{e}^{\prime}, \end{equation}

where $\mathbf{a=}\left( 1,0,\ldots,0\right) $ and $\boldsymbol\Psi=\left[ \begin{array} [c]{ccccc} 1-p_{2}-p_{3} & p_{2} & 0 & \cdots & 0\\ 1-p_{2}-p_{3} & 0 & & \cdots & 0\\ \vdots & & & \ddots & \\ 1-p_{2}-p_{3} & 0 & 0 & \cdots & p_{2}\\ 1-p_{2}-p_{3} & 0 & 0 & \cdots & 0 \end{array} \right] _{k\times k}$.

Proof. $S^{N_{v}^{(k)}+1}= {\displaystyle\sum\limits_{i=1}^{N}} T_{i}$ denotes the amount of time the system operates at its best performance, where N is the number of shocks until k consecutive shocks whose magnitude is between d ₁ and d ₂ or a single shock whose magnitude is greater than $d_{2}, $ that is $N=\min(U_{1},V)$. The proof is completed by using proposition 1 and Lemma 3 in [7].

Theorem 7.

(4)\begin{align} P\left( S-S^{N_{v}^{(k)}+1} \gt s\right) =P\left( S \gt s\right) P\left( V \gt U_{1}\right), \end{align}

and

\begin{equation*} P\left( S-S^{N_{v}^{(k)}+1}=0\right) =P(V \lt U_{1}). \end{equation*}

Proof. From Corollary 4, we have:

\begin{equation*} P\left( S-S^{N_{v}^{(k)}+1} \gt s\right) =P\left( {\displaystyle\sum\limits_{i=1}^{V-U_{1}}} T_{i} \gt s|V \gt U_{1}\right) P\left( V \gt U_{1}\right). \end{equation*}

When $V \gt U_{1}$, $V-U_{1}$ is geometrically distributed having mean $1/p_{3}$. Therefore,

\begin{equation*} P\left( {\displaystyle\sum\limits_{i=1}^{V-U_{1}}} T_{i} \gt s|V \gt U_{1}\right) =P\left( {\displaystyle\sum\limits_{i=1}^{V^{\ast}}} T_{i} \gt s\right) =P\left( S \gt s\right), \end{equation*}

where $P(V^{\ast}=v)=p_{3}(1-p_{3})^{v-1},v=1,2,\ldots$ Thus,

\begin{equation*} P\left( S-S^{N_{v}^{(k)}+1} \gt s\right) =P\left( S \gt s\right) P\left( V \gt U_{1}\right). \end{equation*}

Theorem 8.

(5)\begin{align} P\left( S^{N_{v}^{(k)}+1} \gt s_1,S \gt s_2\right) =P(S \gt s_1)-P(V \gt U_{1})P(S \gt s_2-s_1)\left( 1-P(S^{N_{v}^{(k)}+1} \gt s_1)\right), \end{align}

Proof. When $s_1 \lt s_2,$ the joint distribution of S and $S^{N_{v}^{(k)}+1}$ can be expressed as:

(6)\begin{align} P\left( S^{N_{v}^{(k)}+1}\leq s_1,S\leq s_2\right) & =P\left( S^{N_{v} ^{(k)}+1}\leq s_1,S\leq s_2,N_{v}^{(k)}=0\right) +\nonumber\\ & P\left( S^{N_{v}^{(k)}+1}\leq s_1,S\leq s_2,N_{v}^{(k)}\neq0\right) \nonumber\\ & =P\left( S\leq s_1,N_{v}^{(k)}=0\right) +P\left( S^{N_{v}^{(k)}+1}\leq s_1,S-S^{N_{v}^{(k)}+1}\leq s_2-s_1,N_{v}^{(k)}\neq0\right) \nonumber\\ & =P\left( S\leq s_1|V \lt U_{1}\right) P\left( V \lt U_{1}\right) +\nonumber\\ & P\left( S^{N_{v}^{(k)}+1}\leq s_1,S-S^{N_{v}^{(k)}+1}\leq s_2-s_1|V \gt U_{1}\right) P\left( V \gt U_{1}\right). \end{align}

Clearly,

(7)\begin{equation} P\left( S\leq s_1|V \lt U_{1}\right) =P\left( S^{N_{v}^{(k)}+1}\leq s_1\right). \end{equation}

Conversely, for $V \gt U_{1},$ $V-U_{1}$ and U ₁ are independent random variables and

\begin{equation*} P\left( U_{1}=u,V-U_{1}=a|V \gt U_{1}\right) =p_1^{u-1}(1-p_1)(1-p_3)^{a-1}p_3. \end{equation*}

Thus, from equation (4),

(8)\begin{align} & P\left( S^{N_{v}^{(k)}+1}\leq s_1,S-S^{N_{v}^{(k)}+1}\leq s_2-s_1|V \gt U_{1}\right)\nonumber\\ & =P\left({\displaystyle\sum\limits_{i=1}^{U_{1}}}T_{i}\leq t,{\displaystyle\sum\limits_{i=1}^{V-U_{1}}}T_{i}\leq s_2-s_1|V \gt U_{1}\right) \nonumber\\ & =P\left({\displaystyle\sum\limits_{i=1}^{U_{1}}}T_{i}\leq s_1|V \gt U_{1}\right) P\left({\displaystyle\sum\limits_{i=1}^{V-U_{1}}}T_{i}\leq s_2-s_1|V \gt U_{1}\right) \nonumber\\ & =P\left( S^{N_{v}^{(k)}+1}\leq s_1\right) P\left( S\leq s_2-s_1\right). \end{align}

Using (7) and (8) in (6) one obtains,

\begin{align*} & P\left( S^{N_{v}^{(k)}+1}\leq s_1,S\leq s_2\right) \\ & =P\left( S^{N_{v}^{(k)}+1}\leq s_1\right) \left[ P\left( V \lt U_{1}\right) +P\left( S\leq s_2-s_1\right) \left( 1-P\left( V \lt U_{1}\right) \right) \right]. \end{align*}

The proof follows from:

\begin{equation*} P\left( S^{N_{v}^{(k)}+1} \gt s_1,S \gt s_2\right) =P\left( S^{N_{v}^{(k)}+1} \gt s_1\right) +P\left( S \gt s_2\right) -1+P\left( S^{N_{v}^{(k)}+1}\leq s_1,S\leq s_2\right). \end{equation*}

In Table 1, the expectation of random variables S, $S^{N_{v}^{(k)}+1}$, and $S-S^{N_{v}^{(k)}+1}$ are calculated. It is worth noting that as the value of k increases, so does the duration of the system in a perfect state.

Table 1. Expectation of random variables S, $S^{N_{v}^{(k)}+1}$, and $S-S^{N_{v}^{(k)}+1}$.

3.1. Mean residual life functions

The system’s MRL is defined by:

\begin{equation*} E\left( S-s|S \gt s\right) =\frac{1}{P\left( S \gt s\right) } {\displaystyle\int\limits_{0}^{\infty}} P\left( S \gt s+x\right) dx, \end{equation*}

since the continuous random variable S is non-negative.

The event $\left\{S \gt s\right\} $ denotes the survival of the system beyond time s, which is appropriate for estimating binary systems’ the MRL. Conversely, the expression:

\begin{equation*} E(S-s|S^{N_{v}^{(k)}+1} \gt s), \end{equation*}

captures the system’s mean residual lifetime, conditional on its optimal performance at time s. This expression reveals the expected duration until failure while the system is functioning at its maximum capacity at time s.

Proposition 9.

(9)\begin{align} E(S-s|S^{N_{v}^{(k)}+1} & \gt s)=\frac{1}{P\left( S^{N_{v}^{(k)}+1} \gt s\right) } {\displaystyle\int\limits_{0}^{\infty}} P(S \gt s+x)dx-P(V \gt U_{1}) {\displaystyle\int\limits_{0}^{\infty}} P(S \gt x)dx\nonumber\\ +P(V & \gt U_{1})P(S^{N_{v}^{(k)}+1} \gt s) {\displaystyle\int\limits_{0}^{\infty}} P(S \gt x)dx\nonumber\\ & =\frac{1}{P\left( S^{N_{v}^{(k)}+1} \gt s\right) }\left[ E\left( S-s|S \gt s\right) P\left( S \gt s\right) -P(V \gt U_{1})E(S)\left[ 1-P(S^{N_{v} ^{(k)}+1} \gt s)\!\right]\! \right]. \end{align}

Proof. Using previous theorem,

\begin{align*} E(S-s|S^{N_{v}^{(k)}+1} & \gt s)=\frac{1}{P\left( S^{N_{v}^{(k)}+1} \gt s\right) } {\displaystyle\int\limits_{0}^{\infty}} P\left( S \gt s+x,S^{N_{v}^{(k)}+1} \gt s\right) dx\\ & =\frac{1}{P\left( S^{N_{v}^{(k)}+1} \gt s\right) } {\displaystyle\int\limits_{0}^{\infty}} P\left( S \gt s+x,S^{N_{v}^{(k)}+1} \gt s\right) dx.\\ \text{From equation } (5), \text{we have:} & \\ & =\frac{1}{P\left( S^{N_{v}^{(k)}+1} \gt s\right) } {\displaystyle\int\limits_{0}^{\infty}} \left[ P(S \gt s+x)-P(V \gt U_{1})P(S \gt x)\right. \\& \quad \times \left. \left( 1-P(S^{N_{v}^{(k)}+1} \gt s)\right) \right] dx\\ & =\frac{1}{P\left( S^{N_{v}^{(k)}+1} \gt s\right) }\left[ {\displaystyle\int\limits_{0}^{\infty}} P(S \gt s+x)dx-P(V \gt U_{1}) {\displaystyle\int\limits_{0}^{\infty}} P(S \gt x)dx\right. \\ & \left. +P(V \gt U_{1})P(S^{N_{v}^{(k)}+1} \gt s) {\displaystyle\int\limits_{0}^{\infty}} P(S \gt x)dx \right]. \end{align*}

Remark 10. Using (2) and (3) in (9 ), we have,

(10)\begin{align} E(S-s|S^{N_{v}^{(k)}+1} & \gt s)=\frac{1}{\left( \boldsymbol\zeta\otimes \mathbf{a}\right) \exp\left( \left( \boldsymbol\Lambda\otimes\mathbf{I}+\left( \mathbf{a}^{0} \boldsymbol\zeta\right) \otimes\boldsymbol\Psi\right) s\right) \mathbf{e}^{\prime}}\left[ - \boldsymbol\zeta\exp\left( \left( \boldsymbol\Lambda +\left( 1-p_{3}\right) \boldsymbol\Lambda^{0} \boldsymbol\zeta\right) s\right)\right. \nonumber\\&\left. \quad \times \left( \boldsymbol\Lambda+\left( 1-p_{3}\right) \boldsymbol\Lambda^{0} \boldsymbol\zeta \right) ^{-1}\mathbf{e}^{\prime}-\right.\\ & \left. P(V \gt U_{1})\left( \left( \boldsymbol\zeta\otimes\mathbf{a}\right) \left( \boldsymbol\Lambda+\left( 1-p_{3}\right) \boldsymbol\Lambda^{0}\zeta \right) ^{-1}\mathbf{e}^{\prime}\right) \right. \nonumber\\&\left. \quad \times \left[ 1-\left( \zeta \otimes\mathbf{a}\right) \exp\left( \left( \boldsymbol\Lambda\otimes \mathbf{I}+\left( \mathbf{a}^{0} \boldsymbol\zeta\right) \otimes \boldsymbol\Psi\right) s\right) \mathbf{e}^{\prime}\right] \right]. \nonumber \end{align}

4. Numerical illustrations

In this section, we consider the realistic example of DDoS attacks in [25]. Consider a network client which stores private data of their clients. Such servers are vulnerable to threats. In our model, system states expressed as bandwidths of the server. The volume of DDoS attacks are defined as the magnitude of the shocks. d ₁ and d ₂ denote the thresholds for the volume of the DDoS attacks. When the network is exposed to k consecutive DDoS attacks with volumes between d ₁ and d ₂, the bandwidth of the network will decrease which will affect the response time of the system that leads to a decrease in the functionality of the server. A DDoS attack with a volume of greater than d ₂ will cause the server to shut down. This can be considered as a fatal shock.

Let $p_1=0.25$, $p_2=0.45$ and $p_3=0.3$ be the probabilities that the volume of the DDoS attacks is less than $d_1=100$ megabits per sec (Mbps), between $d_1=$ 100 Mbps and $d_2=1$ gigabits per sec (Gbps), and greater than $d_2=1$ Gbps, respectively. We assume that the bandwidth of the network decreases when two consecutive DDoS attacks having volumes between $d_1=100$ Mbps and $d_2=1$ Gbps occur. Assuming that the inter-arrival times of DDoS attacks $T_{1},T_{2},\ldots$ are exponentially distributed with unit mean, in Figure 2, we plot the MRL of the network traffic when it is known that the network has full bandwidth at time s.

By using equation (10), the effect and sensitivity of k, p ₁ and p ₂ on the MRL when it is known that the system is in the best performance at time s are discussed in Figure 3.

Figure 2. The mean residual life of the network traffic when it is known that the network has full bandwidth at time s.

Figure 3. Effect and sensitivity of k, p ₁ and p ₂ on the mean residual life when it is known that the system is in the best performance at time s.

According to Figure 3, for any value of k, an increase in p ₁ or p ₂ causes $E(S-s|S^{N_{v} ^{(k)}+1} \gt s)$ to increase, while an increase in p ₃ causes $E(S-s|S^{N_{v} ^{(k)}+1} \gt s)$ to decrease.

5. Conclusion

We consider a system that experiences random shocks over time, with two critical levels, d ₁ and d ₂, where $d_1 \lt d_2$. This system is partially damaged if k successive shocks whose magnitude is between d ₁ and d ₂ cause the system to fall to a lower partially functional state. However, a shock with a higher magnitude d ₂ leads to a complete failure of the system. According to our assumption, the time between successive shocks follows a phase-like distribution, which allows us to evaluate the dynamic reliability properties of the multi-state system. This study has generalized the extreme shock model to run a shock model for a multi-state system. According to the results, an increase in the number of consecutive shocks (k) leads to an increase in the MRL when it is known that the system is in the best performance at time s. In addition, for any value of k, a change in p ₁ or p ₂ causes $E(S-s|S^{N_{v}^{(k)}+1} \gt s)$ in the same direction, while a change in p ₃ causes $E(S-s|S^{N_{v}^{(k)}+1} \gt s)$ to change in the opposite direction. Throughout this paper, only the impact of the external shock damage has been considered on the failure of the system. The internal damage degradation of the system has not been considered and modeled. For future studies, the impact from internal degradation may be considered. Also, the multi-state system can be re-modeled with different shock models, such as δ shock models, cumulative shock models or combinations of other types of shock models.