A practical source coding scheme based on approximate string matching is proposed. It is an approximate fixed-length string matching data compression combined with a block-coder based on the empirical distribution. A lemma on approximate string matching, which is an extension of the Kac Lemma, is proved. It is shown, based on the lemma, that the deterministic algorithm converts the stationary and ergodic source, u, into an output process v, and under the assumption that v is a stationary process, after the scheme has run for an infinite time, the optimal compression ratio R(D) is achieved. This reduces the problem of the universal lossy coder to the proof of stationarity of the output process ν in the proposed algorithm. The main advantages of the proposed method are the asymptotic sequential behavior of the encoder and the simplicity of the decoder.

We consider an infinite series of independent and identical -/GI/∞ queues fed by an arbitrary stationary and ergodic arrival process, A1. Let Ai be the arrival process to the ith node, and let νi be the law of Ai. Denote by 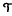(·) the input–output map of the ·/GI/∞ node; that is, νi+1 = 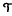(νi). It is known that the Poisson process is a fixed point for 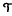. In this paper, we are interested in the asymptotic distribution of the departure process from the nth node, νn+1 = 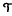n(ν1), as n ∞. Using couplings for random walks, this limiting distribution is shown to be either a Poisson process or a stationary ν-Poisson process, depending on the joint distribution of A1 and the service process. This generalizes a result of Vere-Jones (1968, Journal of the Royal Statistical Society, Series B 30: 321–333) and is similar in flavor to Mountford and Prabhakar (1995, Annals of Applied Probability 5(1): 121–127), where Poisson convergence is established for departures from a series of exponential server queues using coupling methods.

This paper is concerned with overflows in queues fed by Markov fluid input. The results are asymptotic in the number of sources; that is, we let the number of users grow large. The main objectives of this study are to characterize both overflow probability and the “most probable way” in which overflow occurs. Applying large deviations techniques, known results (Weiss, 1986, Advances in Applied Probability 18: 506–532) for exponential on-off sources are extended to general Markov fluid input. Successively, zero, small, and large buffers are treated. Finally, results for multiclass input are given.

Recently, a Pollaczek-Khintchine-like formulation for M/G/l queues with disasters has been obtained. A disaster is said to occur if a negative arrival causes all the customers (and therefore work) to depart from the system immediately. This study generalizes this result further, as it is shown to hold even when negative arrivals cause only part of the work to be demolished. In other words, an arbitrary amount of work, following a known distribution, is allowed to be removed at a negative event. Under these circumstances, a general approach for obtaining the Pollaczek–Khintchine Formula is proposed, which is then illustrated via several examples. Typically, it is seen that the formulainvolves certain parameters that are not explicitly known. The formula itself is made possible due to the number in system being geometric under preemptive last in-first out discipline.

Motivated by two measures of presortedness, number of runs and oscillation of a permutation, related to the sorting problem, we derive an error bound for normal approximation to the distribution of Here, αij's are given real numbers and π is a uniformly distributed random permutation of {l,…, n}. The derivation is based on Stein's method.

Several agents with different subjective probabilities make a binary decision at a time determined by a planner. Each agent chooses the action that has the highest probability of success. Given that their probabilities differ, so will their choices. From time 0 until decision time, all the agents are entitled to access the same increasing flow of information. The planner, who gains from having as many agents as possible making the right choice, faces the following tradeoff: the more information she feeds to the agents, the better off they will be in making their decisions, but the less likely they will be to diversify their actions, so the more difficult it will be for her to hedge her positions. The model gives rise to a continuous time optimal stopping problem.

In this paper, we present some new results on the makespan and flowtime in a two-parallel machine open shop. A set of n jobs is to be processed on two machines, the order of processing being immaterial. For the case where the machines are identical, and the jobs are nonoverlapping ordered, we show that the sequences that stochastically minimize the makespan are longest processing time first-shortest processing time first (LPT-SPT). Within this class of sequences, we show that the SPT sequence stochastically minimizes the flowtime.

We develop a method for computing the optimal double band [b, B] policy for switching between two diffusions with continuous rewards and switching costs. The two switch levels [b, B] are obtained as perturbations of the single optimal switching point a of the control problem with no switching costs. More precisely, we find that in the case of average reward problems the optimal switch levels can be obtained by intersecting two curves: (a) the function, γ(a), which represents the long-run average reward if we were to switch between the two diffusions at a and switches were free, and (b) a horizontal line whose height depends on the size of the transaction costs. Our semianalytical approach reduces, for example, the solution of a problem recently posed by Perry and Bar-Lev (1989, in Stochastic Analysis and Applications 7: 103–115) to the solution of one nonlinear equation.

It is well known that mixtures of decreasing failure rate (DFR) distributions have the DFR property. A similar result is, of course, not true for increasing failure rate (IFR) distributions. In a recent note, Gurland and Sethuraman (1994, Technometrks36(4): 416–418) presented two examples where mixtures of IFR distributions show DFR property. In this paper, we present a general approach to study the mixtures of distributions and show that the failure rates of the unconditional and conditional distributions cross at most at one point. Mixtures of Weibull distribution with a shape parameter greater than 1 are examined in detail. This also enables us to study the monotonic properties of the mean residual life function of the mixture. Some examples are provided to illustrate the results.

We consider a hierarchical linear regression model where the regression parameters for the units have a multivariate normal distribution whose parameters are unknown. Several replications are available for each unit. The design matrices for the units need not be the same. A complicating feature of the model is that each observation is subject to measurement error. The objective of the paper is to derive the predictive distribution of the “true” value of the response at a given design point. A Bayesian treatment is given to the problem. In addition to standard prior distributions, other prior distributions are considered. The calculations are done with the Gibbs sampler. An example is discussed in detail.