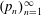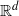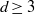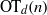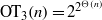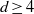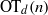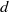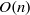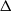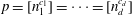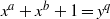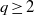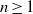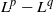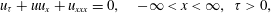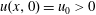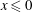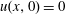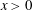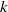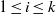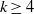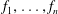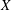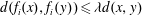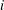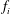Research Article
EXPLICIT BOUNDS ON AUTOMORPHIC AND CANONICAL GREEN FUNCTIONS OF FUCHSIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2014, pp. 257-306
-
- Article
- Export citation
SPECIAL POINT PROBLEMS WITH ELLIPTIC MODULAR SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 06 November 2013, pp. 1-31
-
- Article
- Export citation
NASH-WILLIAMS’ THEOREM ON DECOMPOSING GRAPHS INTO FORESTS
- Part of:
-
- Published online by Cambridge University Press:
- 06 August 2013, pp. 32-36
-
- Article
- Export citation
ON THE METRIC THEORY OF CONTINUED FRACTIONS IN POSITIVE CHARACTERISTIC
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2014, pp. 307-320
-
- Article
-
- You have access
- Export citation
THE TILED CIRCLE PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 31 March 2014, pp. 321-346
-
- Article
- Export citation
A NOTE ON ORDER-TYPE HOMOGENEOUS POINT SETS
- Part of:
-
- Published online by Cambridge University Press:
- 19 December 2013, pp. 37-42
-
- Article
- Export citation
THE ERROR TERM IN THE COUNT OF ABUNDANT NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 02 January 2014, pp. 43-65
-
- Article
- Export citation
THE INTERSECTION OF PIATETSKI-SHAPIRO SEQUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. 347-362
-
- Article
- Export citation
PERFECT POWERS WITH THREE DIGITS
- Part of:
-
- Published online by Cambridge University Press:
- 06 August 2013, pp. 66-84
-
- Article
- Export citation
MULTIPLE EXPONENTIAL AND CHARACTER SUMS WITH MONOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2014, pp. 363-373
-
- Article
- Export citation
THE SQUARE TERMS IN GENERALIZED LUCAS SEQUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 19 December 2013, pp. 85-100
-
- Article
- Export citation
AN AFFINE FOURIER RESTRICTION THEOREM FOR CONICAL SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 13 December 2013, pp. 374-390
-
- Article
- Export citation
Corrigendum
COUNTING RATIONAL POINTS ON CUBIC HYPERSURFACES: CORRIGENDUM
- Part of:
-
- Published online by Cambridge University Press:
- 06 September 2013, pp. 101-107
-
- Article
-
- You have access
- Export citation
Research Article
THE LARGE-TIME DEVELOPMENT OF THE SOLUTION TO AN INITIAL-VALUE PROBLEM FOR THE KORTEWEG–DE VRIES EQUATION. II. INITIAL DATA HAS A DISCONTINUOUS COMPRESSIVE STEP
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2014, pp. 391-414
-
- Article
- Export citation
ALMOST-PRIME
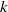 $k$-TUPLES
$k$-TUPLES
- Part of:
-
- Published online by Cambridge University Press:
- 06 September 2013, pp. 108-138
-
- Article
- Export citation
THE FINITE SECTION METHOD FOR DISSIPATIVE OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2014, pp. 415-443
-
- Article
- Export citation
CONVEX CURVES AND A POISSON IMITATION OF LATTICES
- Part of:
-
- Published online by Cambridge University Press:
- 02 January 2014, pp. 139-152
-
- Article
- Export citation
CONTRACTIVE FAMILIES ON COMPACT SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2014, pp. 444-462
-
- Article
- Export citation
ON WARING’S PROBLEM: TWO SQUARES AND THREE BIQUADRATES
- Part of:
-
- Published online by Cambridge University Press:
- 28 June 2013, pp. 153-165
-
- Article
- Export citation
THE ERDŐS–SZEKERES PROBLEM FOR NON-CROSSING CONVEX SETS
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2014, pp. 463-484
-
- Article
- Export citation