Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T07:13:19.768Z Has data issue: false hasContentIssue false
  • English
  • Français

THE INTERSECTION OF PIATETSKI-SHAPIRO SEQUENCES

Part of: Exponential sums and character sums

Published online by Cambridge University Press:  01 April 2014

Roger C. Baker
Roger C. Baker*
Affiliation:
Department of Mathematics, Brigham Young University, Provo, UT 84602,U.S.A. email [email protected]
Get access

Abstract

We give an asymptotic formula for the number of primes 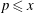$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p \le x$ of the form 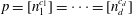$p = [n_1^{c_1}] = \cdots = [n_d^{c_d}]$, where 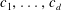$c_1, \ldots, c_d$ are greater than 1 but “sufficiently close” to 1. This improves work of E. R. Sirota 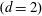$(d=2)$ and W. Zhai 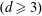$(d \ge 3)$.

MSC classification

Secondary: 11L20: Sums over primes
Type
Research Article
Information
Mathematika , Volume 60 , Issue 2 , July 2014 , pp. 347 - 362
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, R. C., Sums of two relatively prime cubes. Acta Arith. 129 2007, 103–146.Google Scholar
Graham, S. W. and Kolesnik, G., Van der Corput’s Method of Exponential Sums, Cambridge University Press (Cambridge, 1991).CrossRefGoogle Scholar
Harman, G., Small fractional parts of additive forms. Philos. Trans. R. Soc. Lond. A 345 1993, 327–338.Google Scholar
Heath-Brown, D. R., Prime numbers in short intervals and a generalized Vaughan identity. Canad. J. Math. 34 1982, 1365–1377.CrossRefGoogle Scholar
Karacuba, A. A., Estimates for trigonmetric sums by Vinogradov’s method, and some applications. Proc. Steklov Inst. Math. 112 1973, 251–265.Google Scholar
Leitmann, D., Durchschnitte von Piatetski-Shapiro Folgen. Monatsh. Math. 94 1982, 33–44.CrossRefGoogle Scholar
Piatetski-Shapiro, I. I., On the distribution of prime numbers in sequences of the form [f (n)]. Math. Sb. 33 1953, 559–566.Google Scholar
Rivat, J. and Sargos, P., Nombres premiers de la forme [n c]. Canad. J. Math. 53 2001, 414–433.CrossRefGoogle Scholar
Sirota, E. R., Laws for the distribution of primes of the form p = [n c] = [m d] in arithmetic progressions. Zap. Nauchn. Sem. Leningrad Otdel. Mat. Inst. Steklov 121 1983, 94–102.Google Scholar
Zhai, W., On the k-dimensional Piatetski-Shapiro prime number theorem. Sci. China Ser. A 42 1999, 1173–1183.CrossRefGoogle Scholar