Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T05:02:35.279Z Has data issue: false hasContentIssue false
  • English
  • Français

CONVEX CURVES AND A POISSON IMITATION OF LATTICES

Part of: Classical differential geometry Geometry of numbers Discrete geometry General convexity Additive number theory; partitions

Published online by Cambridge University Press:  02 January 2014

Nick Gravin ,
Fedor Petrov ,
Sinai Robins  and
Dmitry Shiryaev
Nick Gravin
Affiliation:
Microsoft Research New England, Cambridge, MA, U.S.A. email [email protected]
Fedor Petrov
Affiliation:
Steklov Mathematical Institute, St.-Petersburg, St.-Petersburg State University,Russia email [email protected] Yaroslavl State University, Russia email [email protected]
Sinai Robins
Affiliation:
Division of Mathematical Sciences, School of Physical and Mathematical Sciences, Nanyang Technological University, Singapore email [email protected] CNRS/LAAS, 7 avenue du Colonel Roche, F-31400 Toulouse,France email [email protected]
Dmitry Shiryaev
Affiliation:
Division of Mathematical Sciences, School of Physical and Mathematical Sciences, Nanyang Technological University,Singapore email [email protected]
Get access

Abstract

We solve a randomized version of the following open question: is there a strictly convex, bounded curve 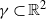$\gamma \subset { \mathbb{R} }^{2} $ such that the number of rational points on 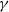$\gamma $, with denominator $n$, approaches infinity with $n$? Although this natural problem appears to be out of reach using current methods, we consider a probabilistic analogue using a spatial Poisson process that simulates the refined rational lattice $(1/ d){ \mathbb{Z} }^{2} $, which we call 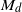${M}_{d} $, for each natural number 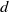$d$. The main result here is that with probability 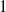$1$ there exists a strictly convex, bounded curve 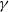$\gamma $ such that 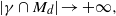$\vert \gamma \cap {M}_{d} \vert \rightarrow + \infty , $ as $d$ tends to infinity. The methods include the notion of a generalized affine length of a convex curve as defined by F. V. Petrov [Estimates for the number of rational points on convex curves and surfaces. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 344 (2007), 174–189; Engl. transl. J. Math. Sci. 147(6) (2007), 7218–7226].

MSC classification

Secondary: 11P21: Lattice points in specified regions 52A10: Convex sets in $2$ dimensions (including convex curves) 52C05: Lattices and convex bodies in $2$ dimensions 53A04: Curves in Euclidean space 52A23: Asymptotic theory of convex bodies 11H06: Lattices and convex bodies
Type
Research Article
Information
Mathematika , Volume 60 , Issue 1 , January 2014 , pp. 139 - 152
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barany, I., Random points and lattice points in convex bodies. Bull. Amer. Math. Soc. 45 (2008), 339–365.Google Scholar
Barany, I. and Reitzner, M., Poisson polytopes. Ann. Probab. 38 (2010), 1507–1531.Google Scholar
Barany, I. and Vershik, A. M., On the number of convex lattice polytopes. Geom. Funct. Anal. 2 (4) (1992), 381–393.Google Scholar
Barany, I. and Vu, V. H., Central limit theorems for Gaussian polytopes. Ann. Probab. 35 (2007), 1593–1621.CrossRefGoogle Scholar
Blaschke, W., Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativit atstheorie: II. Affine Differentialgeometrie, Springer (Berlin, 1923).CrossRefGoogle Scholar
Daley, D. J. and Vere-Jones, D., An Introduction to the Theory of Point Processes, Springer (New York, 1988).Google Scholar
Petrov, F. V., On the number of rational points on a strictly convex curve. Funktsional. Anal. i Prilozhen. 40 (1) (2006), 30–42; Engl. transl., Funct. Anal. Appl. 40(1) (2006), 24–33.Google Scholar
Petrov, F. V., Estimates for the number of rational points on convex curves and surfaces. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 344 (2007), 174–189; Engl. transl., J. Math. Sci. 147(6) (2007), 7218–7226.Google Scholar
Vershik, A. M., The limit form of convex integral polygons and related problems. Funktsional. Anal. i Prilozhen. 28 (1) (1994), 16–25; Engl. transl., Funct. Anal. Appl. 28(1) (1994), 13–20.CrossRefGoogle Scholar