It has long been conjectured that any indefinite quadratic form, with real coefficients, in 5 or more variables assumes values arbitrarily near to 0 for suitable integral values of the variables, not all 0. The basis for this conjecture is the fact, proved by Meyer in 1883, that any such form with rational coefficients actually represents 0.

In 1955 a programme of study of the first 10000 zeros of the Riemann Zeta-function

was completed. Use was made of the high-speed digital computer SWAC and a report of this programme has appeared recently [1]. More recently still, the programme has been extended to the first 25000 zeros. All these zeros have σ= ½ The purpose of this paper is to summarize the methods needed for this (and possibly future) work from the highspeed computer point of view.

Marshall Hall has proved that every real number is representable as the sum of two continued fractions with partial quotients at most 4. This implies that for any real β1, β2 there exists a real α such that

for all integers x > 0 and y, where C is a positive constant. In this note I prove a generalization to r numbers β2, …, βr. The case r = 2 implies a result similar to Marshall Hall's but with a larger number (71) in place of 4.

Let

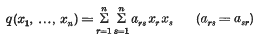
denote an indefinite quadratic form in n variables with real coefficients and with determinant Δn≠0. Blaney ([1], Theorem 2) proved that for any γ ≥0 there is a number Γ = Γ(γ, n) such that the inequalities

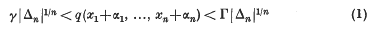
are soluble in integers x1, …, xn for any real α1, …, αn The object of this note is to establish an estimate for Γ as a function of γ. The result obtained, which is naturally only significant if γ is large, is as follows.

In the following pages there will be found an account of the properties of a certain class of local rings which are here termed semi-regular local rings. As this name will suggest, these rings share many properties in common with the more familiar regular local rings, but they form a larger class and the characteristic properties are preserved under a greater variety of transformations. The first occasion on which these rings were studied by the author was in connection with a problem concerning the irreducibility of certain ideals, but about the same time they were investigated in much greater detail by Rees [7] and in quite a different connection. In his discussion, Rees made considerable use of the ideas and techniques of homological algebra. Here a number of the same results, as well as some additional ones, are established by quite different methods. The essential tools used on this occasion are the results obtained by Lech [3] in his important researches concerning the associativity formula for multiplicities. Before describing these, we shall first introduce some notation which will be used consistently throughout the rest of the paper.

Although there is an extensive literature dealing with the location of characteristic roots of matrices, the problem of estimating the maximum distance between two characteristic roots of a given matrix does not appear to have attracted much attention. In the present note we shall be concerned with this problem.

Let (x1, y1), …, (xN, yN) be N points in the square 0 ≤ x < 1, 0 ≤ y < 1. For any point (ξ, η) in this square, let S(ξ, η) denote the number of points of the set satisfying

Let Λ be a lattice in three-dimensional space with the property that the spheres of radius 1 centred at the points of Λ cover the whole of space. In other words, every point of space is at a distance not more than 1 from some point of Λ. It was proved by Bambah that then

equality occurring if and only if Λ is a body-centred cubic lattice with the side of the cube equal to 4/√5. Another way of stating the result is to say that the least density of covering of three-dimensional space by equal spheres, subject to the condition that the centres of the spheres form a lattice, is . Another proof of Bambah's result was given recently by Barnes. Both proofs depend on the theory of reduction of ternary quadratic forms.

A complex-valued function ƒ is said by W. Maak [1] to be almost periodic (a.p.) on Rn if for every positive number ε there is a decomposition of Rn into a finite number of sets S such that

for all h in Rn and all pairs x, y belonging to the same S. This definition is equivalent to that of Bohr when ƒ is continuous.

The problem of a concentrated normal force at any point of a thin clamped circular plate was treated in terms of infinite series by Clebsch [1], who gave the general solution of the biharmonic equation D∇4w = p. Using the method of inversion Michell [2] found a solution for the same problem in finite terms. The method of complex potentials was used by Dawoud [3] to solve the problem of an isolated load on a circular plate under certain boundary conditions. Applying Muskhelishvili's method Washizu [4] obtained the same results for clamped and hinged boundaries. The complex variable method was applied by the authors [5] to obtain solutions for a thin circular plate having an eccentric circular patch symmetrically loaded with respect to its centre under a particular form of boundary condition defining certain types of boundary constraints which include the usual clamped and hinged boundaries as well as other special cases. Flügge [6] gave the solution for a linearly varying load over the complete simply supported circular plate. Using complex variable methods Bassali [7] found the solution for the same load distributed over the area of an eccentric circle under the boundary conditions mentioned before [5], and the authors [8] obtained the solutions for general loads of the type cos nϑ(or sinnϑ), spread over the area of a circle concentric with the plate. In this paper the solutions for a circular plate subjected to the same boundary conditions are obtained when the plate is acted upon by the following types of loading: (a) a concentrated load at an arbitrary point; (b) a line load spread on any part of a diameter; (c) a load distributed over the area of a sector of the plate; (d) a concentrated couple at an arbitrary point of the plate. As a limiting case we find the deflexion at any point of a thin elastic plate having the form of a half plane clamped along the straight edge and subject to an isolated couple at any point.

Subdivision of the fundamental equation of elasticity into two wave equations appears in most text-books on elasticity theory but the two types of vibration are rarely considered independently. Prescott [1] discussed the possibility of the separate existence of plane dilational and distortional waves in semi-infinite material and, failing to satisfy the conditions at a stress-free boundary, concluded that the two types of motion could not exist independently in such circumstances. He therefore derived solutions using combinations of the two types of vibrations. In this paper it is shown that Prescott's solutions are not unique and that special types of purely dilational and purely distortional vibrations are possible in the presence of a free plane boundary. The problem first investigated by Lamb [2] and later by Cooper [3] of transient vibrations of an infinite plate is then considered. In view of the complexity of the equations involved it is worth while attempting to use the subdivision of the fundamental equation to split the problem into simpler problems. In this connection the possibility of dilational or distortional vibrations alone is investigated and a stable form of distortional waves is discovered. It is seen, however, that subdivision of the general problem is not possible.