Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T11:24:34.623Z Has data issue: false hasContentIssue false
  • English
  • Français

Measurable almost periodic functions

Published online by Cambridge University Press:  26 February 2010

H. Kestelman
H. Kestelman
Affiliation:
University College, London.
Get access

Extract

A complex-valued function ƒ is said by W. Maak [1] to be almost periodic (a.p.) on Rn if for every positive number ε there is a decomposition of Rn into a finite number of sets S such that

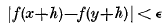
for all h in Rn and all pairs x, y belonging to the same S. This definition is equivalent to that of Bohr when ƒ is continuous.

Type
Research Article
Information
Mathematika , Volume 3 , Issue 2 , December 1956 , pp. 140 - 143
Copyright
Copyright © University College London 1956

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Maak, W., Fastperiodische Funktionen (Springer, Berlin, 1950).CrossRefGoogle Scholar
2.Ursell, H. D., “Normality and almost periodic functions”, Journal London Math. Soc., 4 (1929), 123–127.CrossRefGoogle Scholar
3.Steinhaus, H., “Sur les distances …”, Fundamenta Math., 1 (1920), 93–104.CrossRefGoogle Scholar