Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T05:02:08.799Z Has data issue: false hasContentIssue false
  • English
  • Français

Thin circular plates under certain distributions of normal loading

Published online by Cambridge University Press:  26 February 2010

W. A. Bassali  and
R. H. Dawoud
W. A. Bassali
Affiliation:
Faculty of Science, University of Alexandria, Alexandria, Egypt
R. H. Dawoud
Affiliation:
Faculty of Science, University of Alexandria, Alexandria, Egypt
Get access

Extract

The problem of a concentrated normal force at any point of a thin clamped circular plate was treated in terms of infinite series by Clebsch [1], who gave the general solution of the biharmonic equation D∇4w = p. Using the method of inversion Michell [2] found a solution for the same problem in finite terms. The method of complex potentials was used by Dawoud [3] to solve the problem of an isolated load on a circular plate under certain boundary conditions. Applying Muskhelishvili's method Washizu [4] obtained the same results for clamped and hinged boundaries. The complex variable method was applied by the authors [5] to obtain solutions for a thin circular plate having an eccentric circular patch symmetrically loaded with respect to its centre under a particular form of boundary condition defining certain types of boundary constraints which include the usual clamped and hinged boundaries as well as other special cases. Flügge [6] gave the solution for a linearly varying load over the complete simply supported circular plate. Using complex variable methods Bassali [7] found the solution for the same load distributed over the area of an eccentric circle under the boundary conditions mentioned before [5], and the authors [8] obtained the solutions for general loads of the type 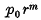cos nϑ(or sinnϑ), spread over the area of a circle concentric with the plate. In this paper the solutions for a circular plate subjected to the same boundary conditions are obtained when the plate is acted upon by the following types of loading: (a) a concentrated load at an arbitrary point; (b) a line load spread on any part of a diameter; (c) a load distributed over the area of a sector of the plate; (d) a concentrated couple at an arbitrary point of the plate. As a limiting case we find the deflexion at any point of a thin elastic plate having the form of a half plane clamped along the straight edge and subject to an isolated couple at any point.

Type
Research Article
Information
Mathematika , Volume 3 , Issue 2 , December 1956 , pp. 144 - 152
Copyright
Copyright © University College London 1956

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Clebsch, A., Theorie der Elastizität fester Körper (Leipzig, 1862).Google Scholar
2.Michell, J. H., Proc. London Math. Soc., 34 (1901).Google Scholar
3.Dawoud, E. H., Ph.D. thesis, London, 1950.Google Scholar
4.Washizu, K., Trans. Soc. Mech. Eng. Japan, 18 (1952), 41.CrossRefGoogle Scholar
5.Bassali, W. A. and Dawoud, R. H., Proc. Cambridge Phil. Soc, 52 (1956), 584–598.CrossRefGoogle Scholar
6.Füigge, W., Bauingenieur, 10 (1929), 221. See Timoshenko's Theory of Plates and Shells, 260.Google Scholar
7.Bassali, W. A., Proc. Cambridge Phil. Soc., 52 (1956), 734–741.CrossRefGoogle Scholar
8.Bassali, W. A. and Dawoud, B. H., Proc. Math. Phys. Soc. Egypt (in the Press).Google Scholar
9.Love, A. E. H., Mathematical Theory of Elasticity (fourth edition, Cambridge, 1934).Google Scholar