Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Coxeter, H. S. M.
Few, L.
and
Rogers, C. A.
1959.
Covering space with equal spheres.
Mathematika,
Vol. 6,
Issue. 2,
p.
147.
1964.
Regular Figures.
p.
327.
Baranovskii, E. P.
1966.
Local minima of the density of the lattice covering of a four-dimensional Euclidean space by similar spheres.
Siberian Mathematical Journal,
Vol. 7,
Issue. 5,
p.
779.
Bambah, R. P.
and
Woods, A. C.
1968.
The covering constant for a cylinder.
Monatshefte f�r Mathematik,
Vol. 72,
Issue. 2,
p.
107.
1969.
Geometry of Numbers.
p.
471.
Baranovskii, E. P.
1971.
Progress in Mathematics.
p.
209.
Saaty, Thomas L.
and
Alexander, Joyce M.
1975.
Optimization and the Geometry of Numbers: Packing and Covering.
SIAM Review,
Vol. 17,
Issue. 3,
p.
475.
Gruber, Peter M.
1979.
Contributions to Geometry.
p.
186.
1987.
Geometry of Numbers.
Vol. 37,
Issue. ,
p.
632.
Bai, Xiaole
Zhang, Chuanlin
Xuan, Dong
Teng, Jin
and
Jia, Weijia
2009.
Low-connectivity and full-coverage three dimensional wireless sensor networks.
p.
145.
Bai, X.
Zhang, C.
Xuan, D.
and
Jia, W.
2009.
Full-Coverage and k-Connectivity (k=14,6) Three Dimensional Networks.
p.
388.
Zhang, Chuanlin
Bai, Xiaole
Teng, Jin
Xuan, Dong
and
Jia, Weijia
2010.
Constructing low-connectivity and full-coverage three dimensional sensor networks.
IEEE Journal on Selected Areas in Communications,
Vol. 28,
Issue. 7,
p.
984.
Xue, F.
and
Zong, C.
2017.
Minkowski bisectors, Minkowski cells and lattice coverings.
Geometriae Dedicata,
Vol. 188,
Issue. 1,
p.
123.
Xue, F.
and
Zong, C.
2018.
On lattice coverings by simplices.
Advances in Geometry,
Vol. 18,
Issue. 2,
p.
181.
Mitsche, Dieter
and
Penrose, Mathew D.
2021.
Limit theory of combinatorial optimization for random geometric graphs.
The Annals of Applied Probability,
Vol. 31,
Issue. 6,
Li, Yiming
Lian, Yanlu
Fu, Miao
and
Zhang, Yuqin
2024.
Lower bound on the translative covering density of octahedra.
Advances in Geometry,
Vol. 24,
Issue. 2,
p.
151.
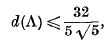
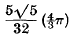 . Another proof of Bambah's result was given recently by Barnes. Both proofs depend on the theory of reduction of ternary quadratic forms.
. Another proof of Bambah's result was given recently by Barnes. Both proofs depend on the theory of reduction of ternary quadratic forms.