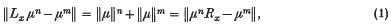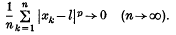Research Article
An irreducible 4-string braid with unknotted closure
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 259-261
-
- Article
- Export citation
Localization in enveloping algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 467-475
-
- Article
- Export citation
Resolving homologies in BPL and PL characteristic numbers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 263-269
-
- Article
- Export citation
Infinitely many disk knots with the same exterior
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 67-72
-
- Article
- Export citation
A characterization of piecewise linear homology manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 271-274
-
- Article
- Export citation
Generalized splitting theorems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 73-86
-
- Article
- Export citation
Pencils of real binary cubics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 477-484
-
- Article
- Export citation
The group of homotopy self-equivalence classes of CW complexes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 275-293
-
- Article
- Export citation
The uniqueness of bundle transfers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 87-111
-
- Article
- Export citation
Transfer and ramified coverings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 485-493
-
- Article
- Export citation
Localization of stable homotopy rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 295-302
-
- Article
- Export citation
Indecomposable knots and concordance
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 495-501
-
- Article
- Export citation
Topological Hopf bifurcation in the plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 113-119
-
- Article
- Export citation
Perturbation of a nest algebra module
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 303-306
-
- Article
- Export citation
Semifinite traces on JBW-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 503-509
-
- Article
- Export citation
Holomorphic sectional curvatures of indefinite complex Grassmann manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 121-125
-
- Article
- Export citation
Topological decompositions of the duals of locally convex operator spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-314
-
- Article
- Export citation
On nearly uniformly convex Banach spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-129
-
- Article
- Export citation
S.I.P. measures on metrizable groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 511-518
-
- Article
- Export citation
FK spaces which include strongly summable sequences
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 131-134
-
- Article
- Export citation

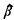 of a braid β ∈
of a braid β ∈ 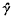 are equivalent as oriented knots. It is a well-known result of Markov, see, for example, (l), that β and γ are closure equivalent if and only if there is a sequence of elementary (Markov) moves in which β ∈
are equivalent as oriented knots. It is a well-known result of Markov, see, for example, (l), that β and γ are closure equivalent if and only if there is a sequence of elementary (Markov) moves in which β ∈ 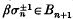 , or
, or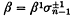 ,
,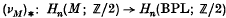 . To show that M bounds, we first ‘resolve the homology to zero’ given by (ν
. To show that M bounds, we first ‘resolve the homology to zero’ given by (ν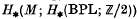 whose vanishing ensures that the homology can be ‘resolved’, i.e. can be replaced by a bordism
whose vanishing ensures that the homology can be ‘resolved’, i.e. can be replaced by a bordism 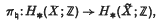
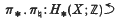
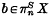 , produces a ring spectrum
, produces a ring spectrum 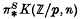 to something more or less trivial, except when
to something more or less trivial, except when 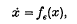
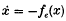 at ∈ > 0 and asymptotic stability of the origin for
at ∈ > 0 and asymptotic stability of the origin for 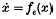 at ∈ < 0 (Hopf (8), Ruelle and Takens(11)) or ∈ = 0 (Chafee(2)).
at ∈ < 0 (Hopf (8), Ruelle and Takens(11)) or ∈ = 0 (Chafee(2)).