Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jacquemard, Alain
1990.
About the effective classification of conjugacy classes of braids.
Journal of Pure and Applied Algebra,
Vol. 63,
Issue. 2,
p.
161.
Birman, Joan S.
and
Menasco, William W.
1992.
Studying links via closed braids. V. The unlink.
Transactions of the American Mathematical Society,
Vol. 329,
Issue. 2,
p.
585.
Fiedler, Thomas
1993.
A small state sum for knots.
Topology,
Vol. 32,
Issue. 2,
p.
281.
Kamada, Seiichi
1996.
On braid monodromies of non-simple braided surfaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 120,
Issue. 2,
p.
237.
BIRMAN, JOAN S.
RAMPICHINI, MARTA
BOLDI, PAOLO
and
VIGNA, SEBASTIANO
2002.
TOWARDS AN IMPLEMENTATION OF THE B–H ALGORITHM FOR RECOGNIZING THE UNKNOT.
Journal of Knot Theory and Its Ramifications,
Vol. 11,
Issue. 04,
p.
601.
Дынников, Иван Алексеевич
and
Dynnikov, Ivan Alekseevich
2003.
Алгоритмы распознавания в теории узлов.
Успехи математических наук,
Vol. 58,
Issue. 6,
p.
45.
Birman, Joan S.
and
Moody, John Atwell
2004.
Obstructions to trivializing a knot.
Israel Journal of Mathematics,
Vol. 142,
Issue. 1,
p.
125.
Birman, Joan S
and
Menasco, William W
2006.
Stabilization in the braid groups I: MTWS.
Geometry & Topology,
Vol. 10,
Issue. 1,
p.
413.
Bangert, Patrick D.
2009.
Lectures on Topological Fluid Mechanics.
Vol. 1973,
Issue. ,
p.
1.
Stoimenow, Alexander
2009.
On non-conjugate braids with the same closure link.
Journal of Geometry,
Vol. 96,
Issue. 1-2,
p.
179.
Stoimenow, A.
2010.
Non-conjugate braids with the same closure link from density of representations.
Journal de Mathématiques Pures et Appliquées,
Vol. 94,
Issue. 5,
p.
470.
SHINJO, REIKO
2010.
NON-CONJUGATE BRAIDS WHOSE CLOSURES RESULT IN THE SAME KNOT.
Journal of Knot Theory and Its Ramifications,
Vol. 19,
Issue. 01,
p.
117.
Iwakiri, Masahide
2011.
Infinite sequences of mutually non-conjugate surface braids representing same surface-links.
Proceedings of the American Mathematical Society,
Vol. 140,
Issue. 1,
p.
357.
Hughes, Mark C
2016.
Braiding link cobordisms and non-ribbon surfaces.
Algebraic & Geometric Topology,
Vol. 15,
Issue. 6,
p.
3707.
Stoimenow, Alexander
2021.
Exchangeability and Non-Conjugacy of Braid Representatives.
International Journal of Computational Geometry & Applications,
Vol. 31,
Issue. 01,
p.
39.
Stoimenow, Alexander
2024.
Subsymmetric exchanged braids and the Burau matrix.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 154,
Issue. 1,
p.
154.
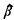 of a braid β ∈ Bn, the braid group on n strings, for some n. Braids β ∈ Bn, γ ∈ Bm are called closure-equivalent if
of a braid β ∈ Bn, the braid group on n strings, for some n. Braids β ∈ Bn, γ ∈ Bm are called closure-equivalent if 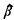 and
and 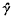 are equivalent as oriented knots. It is a well-known result of Markov, see, for example, (l), that β and γ are closure equivalent if and only if there is a sequence of elementary (Markov) moves in which β ∈ Bn is replaced by
are equivalent as oriented knots. It is a well-known result of Markov, see, for example, (l), that β and γ are closure equivalent if and only if there is a sequence of elementary (Markov) moves in which β ∈ Bn is replaced by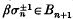 , or
, or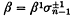 ,
,