Beltrami's discovery that corresponding to any ruled surface there is another applicable on it having corresponding generators parallel but with the parameter of distribution of opposite signs, has brought into prominence the distinction between the applicability of two surfaces and the continuous deformation of one into the other. It is pointed out that since the parameter of distribution differs in sign, the tangent plane rotates in opposite directions as the point of contact proceeds along the two corresponding generators on the respective surfaces. One surface cannot, therefore, be deformed into the other. It is proposed in the present paper to investigate the distinction between applicability and deformability of two surfaces in general, and to connect this isolated fact with the general theory of deformation.

I consider functions of numerical magnitudes ast, where s, t may each assume the values 1,2, … n.

Symmetric functions are those which are unaltered by the whole of the substitutions of the n integers, when they are applied simultaneously to both suffixes.

Stable colloidal sols are always charged, and disperse systems in water appear in most cases to acquire a constant electrokinetic potential of 70 m.v. When the electrokinetic potential falls to 30 m.v. coagulation commences and the rate of coagulation is, as Hardy first pointed out, most rapid at the isoelectric point. Thus the question on what the stability of a colloidal system rests must ultimately be referred to the magnitude of the electrokinetic potential and the methods by which this is increased or decreased in solution.

(1) The conditions of dissociative equilibrium in an external gravitational field have been given by Willard Gibbs, as follows: If the state of a system is such that it is in (mechanical and thermodynamic) equilibrium when the constituents are taken to be independent, and if a condition of dissociative equilibrium is satisfied at one point, then the same condition is satisfied at all points, and the state is one of equilibrium if the constituents are actually capable of dissociating.

(2) In particular, the constituents of a column of dissociating gas under gravity settle out according to Dalton's law; if the condition of dissociative equilibrium is satisfied at one height it is satisfied at all heights.

(3) The conditions of equilibrium are generalised so as to take account of external electric fields and of the possibility of the products of dissociation being charged. Result (1) is shown to be unaffected.

(4) The theory is applied to the equilibrium of an ionized gas such as a stellar atmosphere under gravity. Whatever the charge on the star, the tendency of the light electrons to diffuse away from the heavy ions is almost entirely prevented by the electrostatic forces between them, and the result is the production of a field in the interior capable of supporting half the weight of the positiveions (Pannekoek, Rosseland). For the purposes of this statement the “interior” may be taken to commence at a pressure of 10−24 atmos. It is only above the level corresponding to 10−34 atmos. that electrons and ions separate out according to Dalton's law.

(5) The theory is applied to the equilibrium of an ionized gas under an external electric field. An external applied field of the order of 40,000 volt cm.−1 cannot give rise to potential differences exceeding about 1 volt under the conditions of a typical stellar atmosphere.

§ 1. In the transformation corresponding to constant acceleration, and in the resulting quadratic form, there is an arbitrary constant. In Einstein's formula for central acceleration a mass m defining the acceleration appears, but no arbitrary constant. In seeking to account for, or to repair, the deficiency I retained all constants naturally arising in the integration of the differential equations, and it then appeared that the result could be obtained by transformation. It will be convenient to state the transformation at the outset, and then to examine the differential equations with a view to a clear understanding of the assumptions made in reaching the more general result.

(1) The simplex in a space Sn of order n (or n − 1 dimensions) is a set of n points a1 a2 …an which do not all lie in a subspace of Sn.

The elements of the simplex a1 a2 …an are the n points a1 a2 …an whieh are elements of order one, the lines ar as which are elements or faces of order two, etc., etc., and finally the n primesa1 a2 … ar−1 ar+1 … an which are elements or faces of order n – 1.

The object of this note is to direct attention to an entirely false inference which was drawn from the analysis given in my previous paper with the same title.

§ 1. Most of the methods which have been devised to give an equation of state of more generality than that of Van der Waals differ from the original method used by him in that they refer only to the uniform conditions in the interior of the gas while his had special reference to the conditions at the boundary. In fact, one of the corrections to the perfect gas law introduced by him is due entirely to the existence of a boundary field of force. The question arises as to what physical interpretation is to be given to the more general equation. The methods previously employed leave the interpretation obscure. In this note two new methods of obtaining the equation of state are given, one applicable to the interior of a gas, the other to the boundary. These methods seem to have certain advantages over those previously given in that they lend themselves to a very simple physical interpretation. While the pressure at the boundary of a gas is the same as that in the interior, the word pressure has a different meaning in the two cases. At the boundary, it is due entirely to the motion of the molecules, whereas in the interior part only is due to the motion of the molecules; this part is the same whatever the nature of the molecules and is in fact given by the perfect gas law. The remaining part is due to the stress set up by the existence of intermolecular fields and, although at any given point it is a fluctuating function of the time, it has everywhere within the gas the same statistical mean value. In this paper, it is referred to as the statical pressure to distinguish it from the more usually understood dynamical or momentum pressure.

In a previous paper the values for some lines of the β-ray spectrum of the natural L radiation of radium B have been given. The purpose of the present paper is to show that many of these lines can be accounted for by assuming that rays corresponding to L X-rays, but generated within the atom, act on various atomic levels. Before proceeding to do so, however, it will be advisable to give a fuller account of the experimental methods.

This paper completes an investigation, of which the first part has already been published, into the integrals of a Hamiltonian system which are formally developable about a singular point of the system. Let

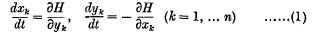
be a system of differential equations of which the origin is a singular point of the first type, i.e. a point at which H is developable in a convergent Taylor series, but at which its first derivatives all vanish. We suppose that H does not involve t, and we consider only integrals not involving t. Let the exponents of this singular point be ± λ1, ± λ2,…±λn. In Part I, I considered the case in which the constants λ1,…λn are connected by no relation of commensurability, i.e. a relation of the form

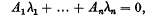
where A1…An are integers (positive, negative or zero) not all zero, and showed that the equations (1) possess n, and only n, integrals not involving t which are formally developable as power series in the xk, yk. In this paper I consider the case in which λ1 … λn are connected by one or more relations of commensur-ability. Suppose that there are p, and only p, such relations linearly independent (p > 0): it will be shown that the equations (1) possess (n − p) independent integrals not involving t, formally developable about the origin and independent of H.

The theorem that, if four arbitrary lines be taken in a plane, the four circles about the triangles formed by threes of these lines, meet in a point, can be generalised to space of any even number of dimensions, as was recognised by Mr J. H. Grace in 1897. In the plane case the centres of the four circles lie on another circle passing through the point of concurrence of these four; it has been sought to prove that the centres of the n + 2 spheres, similarly arising in space of an even number, n, of dimensions, also lie on a sphere†.

The following is a simple example of what Poincaré calls probabilité du continu.

Two points are marked at random on a unit line and it is assumed that all positions of either point are equally probable. What is the average or probable positive distance between the two points?

In two recent papers in the Philosophical Magazine the statistical theory of collisions of electrons with atoms has been considered, and applied to explain the observed features of the capture and loss of electrons by α-particles. The basis of that discussion can however be improved. Firstly, interactions with the core of any atom entered by the α-particle were explicitly ignored. Such interactions—or rather interactions with the general intra-atomic field as distinct from individual electrons—might be expected to be (and are) important, and it has been found possible to include them in this paper. Secondly, the frequency laws for the processes concerned were based on the classical Thomson-Bohr theory of ionization by collision. This theory—it is well known—does not completely reproduce experimental facts at α-particle velocities, and a less restrictive form can be given to the frequency laws which appears to be in accord with all the known facts. The application to the capture and loss of electrons by α-particles proves to be unaffected.

1. In a paper “Beiträge zur Inversionsgeometric,” which will appear in the forthcoming volume of the Science Reports of the Tôhoku Imperial University, I have treated the problem of determining the necessary and sufficient condition in order that two plane curves which are given by natural equations should be transformable into each other by inversion. In connection with that paper I propose here to treat the analogous problem for Laguerre transformations:

Having given two plane curves, by natural equations, in which the functional relations are all supposed to be analytic, it is required to determine the necessary and sufficient condition in order that the two plane curves should be transformable into each other by a Laguerre transformation.

As is well illustrated by photographs of their tracks, the majority of β-particles of given initial velocity bave approximately the same range, measured along the path. When the track shows a visible branch, indicating that an exceptionally close encounter has resulted in the ejection of an electron with kinetic energy amounting to an appreciable fraction of that of tbe primary particle, the main track is naturally of less tban tbe average range. A diminution of range may also be expected to follow such of the nuclear deflections as result in the emission of X radiation; this decrease in range indeed affords a possible method of measuring the energy of the radiation emitted in individuai cases and so testing theories such as that of Kramers as to the nature and origin of the continuous X-ray spectrum.

It is well known that the β-ray type of disintegration is usually accompanied by the emission of γ-rays, and it is a matter of great importance to decide which of these two phenomena occurs first, that is, whether the γ-rays are emitted before the nucleus disintegrates or afterwards. It is not practicable to attempt a direct solution of this problem, but since the emission of the disintegration electron results in a change of the nuclear charge of + 1 it would be sufficient to determine the atomic number of the radioactive body at the moment of emission of the γ-rays. For instance, an atom of the β-ray body radium B has an atomic number 82, but after disintegration when it becomes radium C it has an atomic number 83, so that if the γ-rays were known to be emitted from a body of atomic number 82 it would mean that they were emitted before the disintegration, whereas if the atomic number 83 were found it would show that they were emitted afterwards.

Let

be a system of differential equations in which X1, … Xn are analytic functions independent of t, expansible in convergent series of powers of x1, … xn. Suppose further that not all the functions X1, … Xn vanish when x1 = … = xn = 0. It will be shown in §§ 1–3 that these equations possess (n — 1) independent integrals independent of t, expansible in convergent series of powers of x1, … xn; i.e. functions

such that

identically. In § 4 it is shown how the series for ϕ1,…ϕn−1 may be most directly constructed, and in § 5 is briefly considered the corresponding problem when the origin is a singular point of the equations, i.e. when the expansions of X1,…Xn all begin with terms of the first or higher degrees.

1. Mr J. P. Gabbatt has discussed in the most recent Part of the Proceedingsof this Society the Pedal locus of a simplex in hyperspace. It is, however, possible to regard the pedal property of the circumcircle somewhat differently and so to seek other extensions. Given a circle, any three points on it are vertices of an inscribed triangle, and the feet of the perpendiculars on the sides from any fourth point of the circle are collinear. Is there any curve in space on which an analogous property holds for any five points, viz. that the feet of the perpendiculars from any one upon the faces of the tetrahedron formed by the other four are coplanar?

It will be shown that curves of order n exist in Euclidean space of n dimensions on which any n + 2 points have such a property; but that the curves cannot be real if n is odd.

In three other papers in this number of the Proceedings will be found direct experimental evidence that in a β-ray disintegration the γ-rays are emitted after the electron has been ejected from the nucleus. In this paper we discuss this result in more detail and especially its bearing on the general picture of the β-ray disintegration.

In the course of a series of signal intensity measurements made at Cambridge on the electric waves received from broadcasting stations a marked difference between day and night conditions has been observed. The day-time signals are sensibly constant but marked fluctuations of intensity become apparent about sunset and continue throughout the night. These variations are detectable at Cambridge on the signals from London, where they represent a change in strength of about 5 per cent.