No CrossRef data available.
Involutions on a Normal Quartic Curve in Space of Four Dimensions
Published online by Cambridge University Press: 24 October 2008
Extract
The object of this note is to correct an error in my paper “Extensions of a theorem of Segre's…,” the notation used being the same. The curve C4 dealt with is regarded as given by its canonical representation
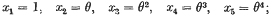
and at one point in the paper we sought the locus of the lines analogous to the line A2A4 of the figure of reference for each of the ∞2 representations of this type (p. 671, small print). In the space representation of the locus there is an additional principal curve

and the order of the locus must be reduced by that of the form corresponding to the points of this conic. The locus sought is in fact none other than the cubic form, locus of chords of C4, the present system of lines being the directrix systemt†. This follows at once from the following results, which can be shown immediately using the above representation:
(1) The space joining such a line g to any tangent cuts the curve again in coincident points, and thus contains a second tangent;
(2) The line joining the points of contact of these tangents meets g, and the points give the involution
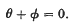
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 1 , February 1924 , pp. 24 - 25
- Copyright
- Copyright © Cambridge Philosophical Society 1924
References
* Proc. Camb. Phil. Soc. XXI, 664 (1923).Google Scholar
† Segre, , “Sulle varietà cubiche…”, Mem. Torino, ser. (2), XXXIX (1889)Google Scholar


