Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T16:55:21.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrals of Systems of Ordinary Differential Equations

Published online by Cambridge University Press:  24 October 2008

T. M. Cherry
T. M. Cherry
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

Let

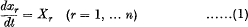
be a system of differential equations in which X1, … Xn are analytic functions independent of t, expansible in convergent series of powers of x1, … xn. Suppose further that not all the functions X1, … Xn vanish when x1 = … = xn = 0. It will be shown in §§ 1–3 that these equations possess (n — 1) independent integrals independent of t, expansible in convergent series of powers of x1, … xn; i.e. functions

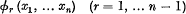
such that

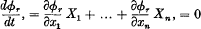
identically. In § 4 it is shown how the series for ϕ1,…ϕn−1 may be most directly constructed, and in § 5 is briefly considered the corresponding problem when the origin is a singular point of the equations, i.e. when the expansions of X1,…Xn all begin with terms of the first or higher degrees.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 3 , 20 September 1924 , pp. 273 - 281
Copyright
Copyright © Cambridge Philosophical Society 1924

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* See, for example, Painlevé, , Léçons sur la théorie analytique des équations différentielles, p. 394.Google Scholar

* “On Integrals developable about a Singular Point of a Hamiltonian System of Differential Equations,” p. 325, below.