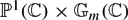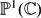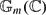Research Article
A heat trace anomaly on polygons
-
- Published online by Cambridge University Press:
- 19 June 2015, pp. 303-319
-
- Article
- Export citation
The Newton tree: geometric interpretation and applications to the motivic zeta function and the log canonical threshold
-
- Published online by Cambridge University Press:
- 12 October 2015, pp. 481-515
-
- Article
- Export citation
The stretch-length tradeoff in geometric networks: average case and worst case study
-
- Published online by Cambridge University Press:
- 05 May 2015, pp. 125-151
-
- Article
- Export citation
Positivity in Kähler–Einstein theory
-
- Published online by Cambridge University Press:
- 25 June 2015, pp. 321-338
-
- Article
- Export citation
An explicit André–Oort type result for
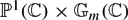 $\mathbb{P}^1(\mathbb{C}) \times \mathbb{G}_m(\mathbb{C})$
$\mathbb{P}^1(\mathbb{C}) \times \mathbb{G}_m(\mathbb{C})$
-
- Published online by Cambridge University Press:
- 30 April 2015, pp. 153-163
-
- Article
- Export citation
The rank of the semigroup of transformations stabilising a partition of a finite set
-
- Published online by Cambridge University Press:
- 06 July 2015, pp. 339-353
-
- Article
- Export citation
Augmented base loci and restricted volumes on normal varieties, II: The case of real divisors
-
- Published online by Cambridge University Press:
- 12 October 2015, pp. 517-527
-
- Article
- Export citation
Portraits of preperiodic points for rational maps
-
- Published online by Cambridge University Press:
- 08 May 2015, pp. 165-186
-
- Article
- Export citation
On the small redshift limit of steady states of the spherically symmetric Einstein–Vlasov system and their stability
-
- Published online by Cambridge University Press:
- 05 October 2015, pp. 529-546
-
- Article
- Export citation
Regularity bounds for complexes and their homology
-
- Published online by Cambridge University Press:
- 02 July 2015, pp. 355-377
-
- Article
- Export citation
Micromeasure distributions and applications for conformally generated fractals
-
- Published online by Cambridge University Press:
- 12 October 2015, pp. 547-566
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 159 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 31 July 2015, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Erratum
Erratum to “On surface links whose link groups are abelian”
-
- Published online by Cambridge University Press:
- 10 April 2015, p. 187
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 159 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 May 2015, pp. f1-f2
-
- Article
-
- You have access
- Export citation
PSP volume 159 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 October 2015, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PSP volume 159 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 31 July 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation
PSP volume 159 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 October 2015, pp. b1-b5
-
- Article
-
- You have access
- Export citation
PSP volume 159 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 May 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation