Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T11:17:00.195Z Has data issue: false hasContentIssue false
  • English
  • Français

The Newton tree: geometric interpretation and applications to the motivic zeta function and the log canonical threshold

Published online by Cambridge University Press:  12 October 2015

PIERRETTE CASSOU-NOGUÈS  and
WILLEM VEYS
PIERRETTE CASSOU-NOGUÈS
Affiliation:
Institut de Mathématiques de Bordeaux, Université Bordeaux I, 350, Cours de la Libération, 33405, Talence Cedex 05, FRANCE e-mail: [email protected]
WILLEM VEYS
Affiliation:
KU Leuven, Dept. Wiskunde, Celestijnenlaan 200B, 3001 Leuven, Belgium e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 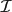${\mathcal I}$ be an arbitrary ideal in ${\mathbb C}$[[x, y]]. We use the Newton algorithm to compute by induction the motivic zeta function of the ideal, yielding only few poles, associated to the faces of the successive Newton polygons. We associate a minimal Newton tree to 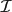${\mathcal I}$, related to using good coordinates in the Newton algorithm, and show that it has a conceptual geometric interpretation in terms of the log canonical model of 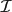${\mathcal I}$. We also compute the log canonical threshold from a Newton polygon and strengthen Corti's inequalities.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 159 , Issue 3 , November 2015 , pp. 481 - 515
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Artal, E., Cassou-Noguès, P., Luengo, I. and Melle Hernández, A. Quasi-ordinary power series and their zeta functions. Mem. Amer. Math. Soc. 178 (2005), vi+85.Google Scholar
[2] Artal, E., Cassou-Noguès, P., Luengo, I. and Melle Hernández, A. ν-Quasi-ordinary power series: factorisation, Newton trees and resultants. Topology of algebraic verieties and singularities. Contemp. Math. 538 (2011), 321–343.Google Scholar
[3] Artal, E., Cassou-Noguès, P., Luengo, I. and Melle Hernández, A. On the log-canonical threshold for germs of plane curves. Singularities I. Contemp. Math. 474 (2008), 1–14.Google Scholar
[4] Corti, A. Singularities of linear systems and 3-fold birational geometry , in Explicit birational geometry of 3-folds. (Cambridge University Press, Cambridge, 2000), 259–312.Google Scholar
[5] Cox, D., Little, J. and Schenck, H. Toric varieties. Graduate Studies in Mathematics, vol. 124 (American Mathematical Society, Providence, RI, 2011).Google Scholar
[6] Campillo, A., Kuhlmann, F. and Teissier, B. (eds). Valuation theory in interaction. EMS Series of Congress Reports, vol. 10 (American Mathematical Society, Providence, RI, 2014).Google Scholar
[7] Cassou-Noguès, P. and Veys, W. Newton trees for ideals in two variables and applications. Proc. London Math. Soc. 108 (2014), 869–910.Google Scholar
[8] de Fernex, T., Ein, L. and Mustaţă, M. Multiplicities and log canonical thresholds. J. Alg. Geom. 13 (2004), 603–615.Google Scholar
[9] Denef, J. and Loeser, F. Motivic Igusa zeta functions. J. Alg. Geom. 7 (1998), 505–537.Google Scholar
[10] Kollar, J. Singularities of pairs. Algebraic Geometry (Santa Cruz 1995). Proc. Sympos. Pure Math. 62 Part 1, 221–287.Google Scholar
[11] Kollár, J. and Mori, S. Birational geometry of algebraic varieties. Cambridge Tracts in Math. 134 (Cambridge University Press, 2008).Google Scholar
[12] Kollár, J., Smith, K. and Corti, A. Rational and nearly rational varieties. Camb. Stud. Adv. Math. 92 (Cambridge University Press, Cambridge, 2004).Google Scholar
[13] Lê, D.T. and Oka, M. On resolution complexity of plane curves. Kodai Math. J. 18 (1996), 1–36.Google Scholar
[14] Mustaţă, M. IMPANGA lecture notes on log canonical thresholds. Notes by Tomasz Szemberg, EMS Ser. Congr. Rep., Contributions to algebraic geometry. Eur. Math. Soc. (Zürich, 2012), 407–442.Google Scholar
[15] Nicaise, J. and Sebag, J. Greenberg approximation and the geometry of arc spaces. Comm. Alg. 38 (2010), 4077–4096.Google Scholar
[16] Swanson, I. and Huneke, C. Integral closure of ideals, rings, and modules. Lond. Math. Soc. L.N.S. 336 (2006).Google Scholar
[17] Van Proeyen, L. and Veys, W. Poles of the topological zeta function associated to an ideal in dimension two. Math. Z. 260 (2008), 615–627.Google Scholar
[18] Van Proeyen, L. and Veys, W. The monodromy conjecture for zeta functions associated to ideals in dimension two. Ann. Inst. Fourier 60 (2010), 1347–1362.Google Scholar
[19] Veys, W. Zeta functions for curves and log canonical models. Proc. London Math. Soc. 74 (1997), 360–378.Google Scholar
[20] Veys, W. Zeta functions and ‘Kontsevich Invariants’ on singular varieties. Canad. J. Math. 53 (2001), 834–865.Google Scholar
[21] Veys, W. and Zúñiga-Galindo, W. Zeta functions for analytic mappings, log-principalization of ideals, and Newton polyhedra. Trans. Amer. Math. Soc. 360 (2008), 2205–2227.Google Scholar