The Hopf-James invariants are a series of homomorphisms

(see (3) or (13)). I. M. James (7) and H. Toda (13), have shown effectively that in the case n even and r a prime p the restrictions to the p-primary components may be embedded in exact sequences

In this note we show that there are similar exact sequences if n is even and r = pq or if n is odd and r = 2pq, and we establish connexions in certain cases between the homomorphisms Hmn and the composite homomorphisms HmHn. We are able to compute the action of the invariants on the groups of the r-stem for r ≤ 9 with the partial exception of π6(S2) and π7(S2). The exact sequences yield useful criteria for determining the reduced product filtrations (see (9)) of elements.

Fuchs((1), Problem 22) has asked the following question: Given positive integers ri (1 ≤ i ≤ 4) such thatr1 + r2 = r3 + r4, r1 ≠ r3, r1 ≠ r4, do there exist indecomposable torsion-free Abelian groups Gi (1 ≤ i ≤ 4) such that, where Gi is of rank ri (1 ≤ i ≤ 4)?* We shall show in this note that there do always exist groups Gi with the desired properties; in fact, we shall prove the following stronger result

If X is a space with base point, let ΩX denote the space of loops of X based at its base point. We will denote the homology and cohomology suspensions by σ* and σ*, respectively, , . Let K(π, n) be the Eilenberg-MacLane complex with only one non-vanishing homotopy group πn(K(π, n))= π, πi(K(π, n)) = 0 for i ≠ n. If π is abelian K(π, n) = ΩK(π, n+1). We will assume that π is a finitely generated abelian group throughout this note. Let K(π, n) × K(π, n) → K(π, n) denote the multiplication in K(π, n).

Let Λ be a commutative ring with an identity element and c an element of Λ which is not a zero divisor Denote by Ω the residue class ring Λ/Λc. If now M is a Λ-module for which c is not a zero divisor, and A is an Ω-module, then a theorem of Rees (2) asserts that, for every non-negative integer n, we have a Λ-isomorphism

This reduction theorem has found a number of useful and interesting applications.

The present paper has been inspired by a theorem of Swan(5). The theorem can be described as follows. Let G be a finite group and let Γ be its integral group ring. We shall denote by Z an infinite cyclic additive group considered as a left Γ-module by defining gm = m for all g in G and m in Z. By a Tate resolution of Z is meant an exact sequence

where Xn is a projective module for − ∞ < n < + ∞, and

.

If X is a compact Hausdorff space we denote by S(X), and by C(X), the hyperspaces of X consisting of all non-empty closed sets, and all non-empty connected closed sets. The topology in each case is the finite topology of Michael ((6), Definition 1·7), in which a sub-base for the open sets is taken consisting of all sets of either of the forms {F|F ⊂ G} and {F|F ∩ G ≠ φ} (where G is any open set of X). Michael has shown that S(X) is also compact Hausdorff ((6), Theorem 4·9·6), and S(X) contains in an obvious way sets which are homeomorphic with C(X) and X itself. We recall that if Xis also a metric space, the topology induced on S(X) (and on C(X)) by Hausdorff's metric is the same as the finite topology ((6), Proposition 3·6).

The purpose of this paper is to investigate the structure of certain types of semigroups. Rees(6),(7) has determined the structure of a completely simple semigroup, and has shown that such a system may be realized as a type of matrix semigroup. Clifford (2) and Schwarz (8) have found conditions, namely, the existence of minimal left and minimal right ideals, under which a simple semigroup is completely simple, and have made a more detailed study of such semigroups. Preston (4), (5) has studied inverse semigroups, in which each non-zero element has a unique relative inverse, and has also considered inverse semigroups which contain minimal right or left ideals. In the present paper we obtain a set of conditions on a simple semigroup, each of which is equivalent to the semigroup being both completely simple and inverse. Section 2 defines the terms used and gives a brief resume of the main results which have already been proved. Section 3 is devoted to our present considerations.

Several relations between the Cesàro and the Riemann methods of summation are known. For instance, Verblunsky(3) has shown that a series summable (C, k − δ), where k is a positive integer, is also summable (R,k+ 1) and Kuttner (2) has proved that, for k = 1, 2, summability (R, k) implies summability (C, k + δ). In this paper we consider Riesz's typical means and a generalized Riemann summability both of which are intimately connected with almost periodic functions. The result we establish is similar to Verblunsky's, except that we start from a Riesz mean of integral order k*.

In a recent paper on the behaviour of a system of disk dynamos(1), a problem of a purely algebraic character arose. The problem is to find all the real solutions of the non-linear, inhomogeneous system of 2n equations

where x0 = xn and the parameter ρ is real and not zero, but otherwise arbitrary. The real solutions were correctly given in (1), but the proof that they are the only real solutions was incomplete. A different, and complete, proof is given here.

It is worth remarking that if e, f are two primitive idempotents in a semigroup S which commute, then: (i) if S has a zero 0, either e = f or ef = 0; (ii) if S has no zero, e = f. Clearly the product ef is under each of the primitive idempotents e and f.

Let {λn} be a sequence of non-negative numbers increasing to infinity. Let be any series. Following the usual terminology, we say that the series is summable (R, λn, k) to s if as u → ∞, where . If, further, u−kA(k)(u) is of bounded variation in (0, ∞), we say that the series is summable s. We say that the series is summable (A, λn) to s if converges for all σ > 0, and tends to s as σ →0+. If A, B are two summability methods, we write A → B (‘A implies B’) if they have the property that any series summable A is necessarily summable B to the same sum.

Given † probability vector μ(X) = (μ1(X), … μk (X)) of a finite number of components on a Borel class of sets X, we say that μ(X0) has a diagonal value α if μi(X0) = α for all i = 1, 2,…,K. J. Neyman(l), (2), (3) has proved that in the class of Borel sets of real numbers any non-atomic vector μ(X) takes all diagonal values. A. Liapounoff has studied the full range of values of k-dimensional vector-valued measures and in two papers (4) he has proved that the range is closed and in the case of non-atomic measures the range is also convex. He also gave an example showing that neither of these results holds in the case of vectors of infinitely many components. A simplified proof of Liapounoff's results has been given by P. R. Halmos (5). In the present paper I study the range of values of probability vectors of infinitely many components. Various types of conditions are studied which are sufficient to imply that, for each ε > 0, 0 ≤ α ≤ 1, it is possible to find a set X such that

Ramanujan's Continued Fraction may be stated as follows: Let where there are eight gamma functions in each product and the ambiguous signs are so chosen that the argument of each gamma function contains one of the specified number of minus signs. Then where the products and the sums on the right range over the numbers α, β, γ, δ, ε: provided that one of the numbers β, γ, δ, ε is equal to ± ±n, where n is a positive integer. In 1935, Watson (3) proved the theorem by induction and also gave a basic analogue. In this paper we give a new proof of Ramanujan's Continued Fraction by using the transformation of Bauer and Muir in the theory of continued fractions (Perron (1), §7;(2), §2).

The problem discussed here arose in the course of some reflections on the critical point theory of Lusternik and Schnirelmann (4). In (4) it is shown how it is possible to associate, with a suitably differentifiable real-valued function f defined on a compact manifold M, a set of real numbers λ1 ≤ λ2 ≤ … λc, which are critical levels of f and which in certain respects are analogous to, and indeed generalizations of, the eigenvalues of a quadratic form. The number c depends on M and is called the category of M. If Rn is Euclidean n-space, Sn the unit sphere of Rn+1, and Pn the real projective n-space obtained from Sn by identifying opposite points, then a quadratic form φ in the (n + 1) coordinates of Rn+1 defines a real function on Sn and, by passage to the quotient, on Pn. Pn has category n + 1, and the numbers λ in this case are just the eigenvalues of the quadratic form.

This note is concerned with a method by which generalized solutions can be shown to exist for certain types of integral equations

where f(x) ∈ L2(0, ∞). The method is briefly this. An extended meaning is given to such equations by using generalized functions of a particular type. Then, if (1) denotes a transformation which has no everywhere-defined inverse in the usual sense, it may be possible to define in the extended sense an inverse transformation

so that if f is given, a generalized function g = can be determined as a solution of (1).

Littlewood has shown(1) that any rotation in 4 dimensions can be expressed as the resultant of a right-handed and a left-handed rotation, and that every right-handed rotation commutes with every left-handed rotation. It follows that the rotation group in 4 dimensions is expressible in some way as the product of two groups of right-handed and left-handed rotations, respectively.

If the components x1, x2,…, xk of a vector X have a non-singular multivariate normal distribution having a null vector of means and variance-covariance matrix Σ= σ2, the matrix R=[ρij] (where ρii = 1) is known in certain cases but σ2 is unknown. If s2 is an estimate of σ2 based on ƒ degrees of freedom and is distributed independently of X, the distribution of the vector t=x/s is known as the multivariate t-distribution. This distribution was first obtained by Dunnett and Sobel (6) and independently by Cornish (3). Dunnett, Sobel and Bechhofer(2) have discussed some practical applications of this distribution. Cornish (3) obtained this distribution while considering the pre-treatment to be given to certain types of replicated experiments. This distribution possesses some useful properties and makes it suitable as a basis for exact tests of significance in various problems, and Dunnett and Sobel (6), by providing tables of the probability integral, have taken the first step towards its use in practice. Cornish, in a later paper (4) considered the sampling distribution of statistics derived from the multivariate t-distribution and using this he obtained the well-known ((7), (8)) distribution of the sample regression coefficient of one variate with respect to another, when both have a bivariate normal distribution.

In this paper an n-stepped self-avoiding walk is defined to be an ordered sequence of n + 1 mutually distinct points, each with (positive, negative, or zero) integer coordinates in d-dimensional Euclidean space (where d is fixed and d ≥ 2), such that any two successive points in the sequence are neighbours, i.e. are unit distance apart. If further the first and last points of such a sequence are neighbours, the sequence is called an (n + 1)-sided self-avoiding polygon. Clearly, under this definition a polygon must have an even number of sides. Let f(n) and g(n) denote the numbers of n-stepped self-avoiding walks and of n-sided self-avoiding polygons having a prescribed first point. In a previous paper (3), I proved that there exists a connective constant K such that

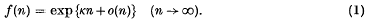
Here I shall prove the truth of the long-standing conjecture that

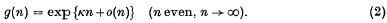
I shall also show that (2) is a particular case of an expression for the number of n-stepped self-avoiding walks with prescribed end-points, a distance o(n) apart, this being another old and popular conjecture.

Drazin (2) has recently introduced the concept of a pseudo-invertible element of an associative ring or semigroup. In this note we first show that such an element of a semigroup S may be characterized by the fact that some power of it lies in a subgroup of S. The main result (Theorem 2) provides a new criterion for complete simplicity: a simple semigroup is completely simple if and only if all its elements are pseudo-invertible. This is applied to the principal factors of a general semigroup and two previously known results are obtained as corollaries.

Following Hardy and Titchmarsh(1) a function f(x) is said to be self-reciprocal if it satisfies the Fourier-Bessel integral transform

where Jp(x) is a Bessel function of order P ≥ –½. This integral is denoted by Rp. The special cases P ½ and P ½, we denote by Rs and Rc, respectively.