Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T05:39:57.597Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Additive Cohomology Operations which are not Suspensions

Published online by Cambridge University Press:  24 October 2008

William Browder
William Browder
Affiliation:
Cornell University and Mathematical InstituteOxford
Get access Rights & Permissions [Opens in a new window]

Extract

If X is a space with base point, let ΩX denote the space of loops of X based at its base point. We will denote the homology and cohomology suspensions by σ* and σ*, respectively, 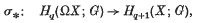, 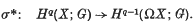. Let K(π, n) be the Eilenberg-MacLane complex with only one non-vanishing homotopy group πn(K(π, n))= π, πi(K(π, n)) = 0 for i ≠ n. If π is abelian K(π, n) = ΩK(π, n+1). We will assume that π is a finitely generated abelian group throughout this note. Let K(π, n) × K(π, n) → K(π, n) denote the multiplication in K(π, n).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 1 , January 1961 , pp. 50 - 54
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bott, R., and Samelson, H., On the Pontryagin product in spaces of paths. Comment. Math. Helvet. 27 (1953), 320–37.CrossRefGoogle Scholar
(2)Cartan, H., Seminaire, H. Cartan 1954–55 (Paris, 1955).Google Scholar
(3)Guggenheim, V. K. A. M., and Moore, J. C., Acyclic models and fibre spaces. Trans. Amer. Math. Soc. 85 (1957), 265–306.CrossRefGoogle Scholar
(4)Kudo, T., A transgression theorem. Mem. Fac. Sci. Kyūsyū Univ. Ser. A, 9 (1956), 79–81.Google Scholar
(5)Moore, J. C., On the homology of K(π, n). Proc. Nat. Acad. Sci., U.S.A. 43 (1957), 409–11.CrossRefGoogle ScholarPubMed
(6)Serre, J.-P., Homologie singulière dea espaces fibrés. Ann. Math. 54 (1951), 425–505.CrossRefGoogle Scholar
(7)Suzuki, H., On the Eilenberg-MacLane invariants of loop spaces. J. Math. Soc. Japan, 8 (1956), 40–48.Google Scholar