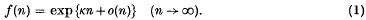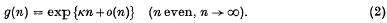Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rushbrooke, G. S.
and
Eve, J.
1962.
High-Temperature Ising Partition Function and Related Noncrossing Polygons for the Simple Cubic Lattice.
Journal of Mathematical Physics,
Vol. 3,
Issue. 1,
p.
185.
Kesten, Harry
1963.
On the Number of Self-Avoiding Walks.
Journal of Mathematical Physics,
Vol. 4,
Issue. 7,
p.
960.
Frisch, H. L.
and
Hammersley, J. M.
1963.
Percolation Processes and Related Topics.
Journal of the Society for Industrial and Applied Mathematics,
Vol. 11,
Issue. 4,
p.
894.
Domb, C.
1964.
Some Statistical Problems Connected with Crystal Lattices.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 26,
Issue. 3,
p.
367.
Kesten, Harry
1964.
On the Number of Self-Avoiding Walks. II.
Journal of Mathematical Physics,
Vol. 5,
Issue. 8,
p.
1128.
Fisher, Michael E.
and
Gaunt, David S.
1964.
Ising Model and Self-Avoiding Walks on Hypercubical Lattices and "High-Density" Expansions.
Physical Review,
Vol. 133,
Issue. 1A,
p.
A224.
Fisher, Michael E.
1966.
Effect of Excluded Volume on Phase Transitions in Biopolymers.
The Journal of Chemical Physics,
Vol. 45,
Issue. 5,
p.
1469.
Martin, J. L.
Sykes, M. F.
and
Hioe, F. T.
1967.
Probability of Initial Ring Closure for Self-Avoiding Walks on the Face-Centered Cubic and Triangular Lattices.
The Journal of Chemical Physics,
Vol. 46,
Issue. 9,
p.
3478.
Domb, Cyril
1969.
Advances in Chemical Physics.
Vol. 15,
Issue. ,
p.
229.
Whittington, S. G.
and
Valleau, J. P.
1969.
Estimation of the Number of Self-Avoiding Lattice Polygons.
The Journal of Chemical Physics,
Vol. 50,
Issue. 11,
p.
4686.
Kumbar, Mahadevappa
and
Windwer, Stanley
1969.
Direct Enumeration Study of Self-Avoiding Walks on the Tetrahedral Lattice.
The Journal of Chemical Physics,
Vol. 50,
Issue. 12,
p.
5257.
Domb, C
and
Hioe, F T
1970.
The transition matrix approach to selfavoiding walks.
Journal of Physics C: Solid State Physics,
Vol. 3,
Issue. 11,
p.
2223.
Domb, C
1970.
Self-avoiding walks and the Ising and Heisenberg models.
Journal of Physics C: Solid State Physics,
Vol. 3,
Issue. 2,
p.
256.
Shante, Vinod K.S.
and
Kirkpatrick, Scott
1971.
An introduction to percolation theory.
Advances in Physics,
Vol. 20,
Issue. 85,
p.
325.
McKenzie, D S
and
Moore, M A
1971.
Shape of self-avoiding walk or polymer chain.
Journal of Physics A: General Physics,
Vol. 4,
Issue. 5,
p.
L82.
Economou, E. N.
and
Cohen, Morrel H.
1972.
Existence of Mobility Edges in Anderson's Model for Random Lattices.
Physical Review B,
Vol. 5,
Issue. 8,
p.
2931.
van Beijeren, H.
and
Gallavotti, G.
1972.
The phase separation line in the two-dimensional Ising model and its relationship with the nonfree-random-walk problem.
Lettere Al Nuovo Cimento Series 2,
Vol. 4,
Issue. 14,
p.
699.
McKenzie, D S
1973.
The end-to-end length distribution of self-avoiding walks.
Journal of Physics A: Mathematical, Nuclear and General,
Vol. 6,
Issue. 3,
p.
338.
Hioe, F. T.
and
Domb, C.
1974.
Group theory, Markov chains, and excluded volume effect in polymers.
Journal of Statistical Physics,
Vol. 10,
Issue. 3,
p.
183.
Whittington, Stuart G.
1975.
Self-avoiding walks terminally attached to an interface.
The Journal of Chemical Physics,
Vol. 63,
Issue. 2,
p.
779.