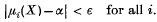No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Given † probability vector μ(X) = (μ1(X), … μk (X)) of a finite number of components on a Borel class of sets X, we say that μ(X0) has a diagonal value α if μi(X0) = α for all i = 1, 2,…,K. J. Neyman(l), (2), (3) has proved that in the class of Borel sets of real numbers any non-atomic vector μ(X) takes all diagonal values. A. Liapounoff has studied the full range of values of k-dimensional vector-valued measures and in two papers (4) he has proved that the range is closed and in the case of non-atomic measures the range is also convex. He also gave an example showing that neither of these results holds in the case of vectors of infinitely many components. A simplified proof of Liapounoff's results has been given by P. R. Halmos (5). In the present paper I study the range of values of probability vectors of infinitely many components. Various types of conditions are studied which are sufficient to imply that, for each ε > 0, 0 ≤ α ≤ 1, it is possible to find a set X such that