Research Notes
A Series associated with an identity of Orr
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 900-901
-
- Article
- Export citation
Research Article
Some consequences of bond alternation in long polyenes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 353-363
-
- Article
- Export citation
Research Notes
A problem on tangents to a sphere
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 685-686
-
- Article
- Export citation
Back matter
PSP volume 57 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
The low-frequency scattering by a perfectly conducting strip
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 364-366
-
- Article
- Export citation
Research Notes
On a problem of Steinhaus about polygons
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 686-688
-
- Article
- Export citation
The single server queue in heavy traffic
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 902-904
-
- Article
- Export citation
Research Article
On some dual series equations and their application to electrostatic problems for spheroidal caps
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 367-384
-
- Article
- Export citation
Research Notes
The mathematical equivalence of the born approximation and the method of impact parameters
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 904-905
-
- Article
- Export citation
Topological embeddings of lens spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 688-690
-
- Article
- Export citation
Some self-reciprocal functions and kernels
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 690-692
-
- Article
- Export citation
Proceedings at the meetings
Proceedings at the Meetings Held During the Session 1960–1961: Annual General Meeting
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 906-909
-
- Article
- Export citation
Research Article
The potential of a circular current
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 385-392
-
- Article
- Export citation
Research Notes
The number of real zeros of the solution of a linear homogeneous differential equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 693-694
-
- Article
- Export citation
Research Article
Vertex generated waves outside metallic wedges
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 393-400
-
- Article
- Export citation
Statement of accounts
Cambridge philosophical society statement of accounts for the year ended 31 December 1960
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 910-912
-
- Article
- Export citation
Research Article
Unsymmetrical flow patterns past a finite wedge profile in a High subsonic stream
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-414
-
- Article
- Export citation
Research Notes
A remark on the proof of dispersion relations in quantum field theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 694-695
-
- Article
- Export citation
Front matter
PSP volume 57 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Research Article
The effects of surface tension and viscosity on the stability of two superposed fluids
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 415-425
-
- Article
- Export citation

 and
and  and on the π-electron contribution
and on the π-electron contribution  to the diamagnetic susceptibility of a cyclic even hydrocarbon polyene
to the diamagnetic susceptibility of a cyclic even hydrocarbon polyene  is investigated. Power series expansions and asymptotic expressions are given for
is investigated. Power series expansions and asymptotic expressions are given for  and χ
and χ

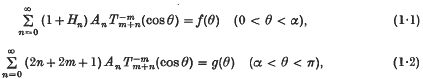
 is the associated Legendre function of degree
is the associated Legendre function of degree  . These latter equations have, however, been discussed in a recent paper by Tranter (13).
. These latter equations have, however, been discussed in a recent paper by Tranter (13).
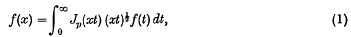
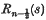 of which, though not Legendre functions, are related to them by the identity (§4·2)
of which, though not Legendre functions, are related to them by the identity (§4·2) 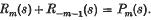

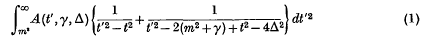
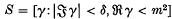 . It was only proved explicitly in (1) that
. It was only proved explicitly in (1) that 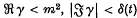 , where δ may depend on
, where δ may depend on