The Hilbert transform, Hf, of a function f is defined by Hf = g, where

P denoting the Cauchy principal value and the integral being assumed to exist in some sense. When f is suitably restricted, Hf exists and

In the first part of Theorem 1 sufficient conditions are given for the validity of (1·2) rather more general than those of Wood ((6), p. 31). The present proof is based on the well-known condition of Riesz for the validity of (1·2), namely, that f is Lp(−∞, ∞) for some p > 1, and on the ‘Parseval’ relation (Lemma 3, (b)), which was used in a similar way by Hardy ((3), p. 110).

Although there are many variations of finite-difference methods of obtaining approximate numerical solutions to ordinary differential equations they share the common feature that they tend to treat an equation of a given type as a standard problem and take no account of any special characteristics the wanted solution may have. We here suggest an alternative procedure when the wanted solution exhibits exponential characteristics. In essence the idea is that if a differential equation has an exponential type solution y(x) it is useful to solve numerically, instead of the equation for y, the equation for u = logey. The error-building and stability characteristics are then those of u rather than y and consequently the accuracy of the solutions may be improved. Although there is nothing basically new in this, of course, the point that we demonstrate is that the differential equation in y can be solved numerically in such a manner that the transformation from y to u is not actually carried out, i.e. we retain the original dependent variable but take account of the exponential variation by modifying the integration formula. Consider for example, in the usual notation, the first-order equation

with a given initial condition y(x0) = y0. If x0, x1, …, xr, xn is a set of pivotal values of x;, usually assumed equally spaced so that xr+1 − xr = h, the usual approach replaces (1) by the formula

which, once the integral is expressed in terms of pivotal values of f using a difference series, represents a step-by-step formula for constructing successive values of y.

The determination of the number of zeros of a complex polynomial in a half-plane, in particular in the upper and lower, or right and left, half-planes, has been the subject of numerous papers, and a full discussion, with many references, is given in Marden (l) and Wall (2), where the basis for the determination is a continued-fraction expansion, or H.C.F. algorithm, in terms of which the number of zeros in one of the half-planes can be written down at once. In addition, determinantal formulae for the relevant elements of the algorithm can be obtained, and these lead to determinantal criteria for the number of zeros, including that of Hurwitz (3) for the right and left half-planes.

The problem of diffusion from an instantaneous point source in a thin plane sheet which is intersected by one or more other thin plane sheets of the same material is considered. This problem arises in the study of the diffusion of packets of transmitter substance in synaptic clefts, and some numerical results for the amphibian neuro-muscular junction are presented. A similar discussion applies to branching rods and to cases where there is loss of diffusing substance at the surfaces of the sheets.

The idea of gauge-invariance in general relativity was first introduced by Weyl(1) who proposed that the field equations of gravitation should be invariant, not only under the general group of coordinate transformations, but also under the gauge-transformation

where is the symmetric metric tensor, is the symmetric affine connexion and λ(x8) is an arbitrary scalar function of the coordinates. In this way it was possible to introduce into the theory a four-vector Ak which in consequence of (1·1) transformed as

such that the six-vector remained an invariant quantity under the gauge-transformation. It was Weyl's hope that by widening the invariance properties gauge-transformation. It was Weyl's hope that by widening the invariance properties of general relativity in this way the vector Ak and its associated six-vector Fik could be interpreted as representing the electromagnetic field. However, no obvious or unique way of doing this was found. More recently (see Stephenson (2,3) and Higgs (4)) gaugeinvariant variational principles formed from Lagrangians quadratic in the Riemann—Christoffel curvature tensor and its contractions have been discussed by performing the variations with respect to the symetric and symetric independently (following the palatini method).

Conditions are examined under which plane shook waves of constant strength can propagate through a gas in a given homentropic motion. Since the entropy change across the shock is taken to be constant homentropic flow exists behind the shock also. The motion behind the shock is determined by solving a Cauchy problem with data given on the back of the shock. The theory is illustrated by two examples, one of which generalizes a result obtained by Copson.

A generalization to two independent variables of Lagrange's expansion of an inverse function was given by Stieltjes and proved rigorously by Poincaré. A new method of proof is given here that also provides a new and sometimes more convenient form of the generalization. The results are given for an arbitrary number of independent variables. Applications are pointed out to random branching processes, to queues with various types of customers, and to some enumeration problems.

This paper demonstrates the existence of an infinity of saddle-points of the function and gives a method of evaluating them suitable for automatic computation. A table of about 100 points is given to 5 decimal places.

In this paper we shall be concerned with the differential equation

in which a and b are constants, p(t) is a continuous periodic function of t with a least period ω, and dots indicate differentiation with respect to t. The function h(x) is assumed continuous for all x considered, so that solutions of (1) exist satisfying any assigned initial conditions. In an earlier paper (2) explicit hypotheses on (1) were established, in the two distinct cases:

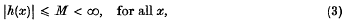
under which every solution x(t) of (1) satisfies

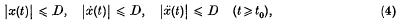
where t0 depends on the particular x chosen, and D is a constant depending only on a, b, h and p. These hypotheses are, in the case (2),

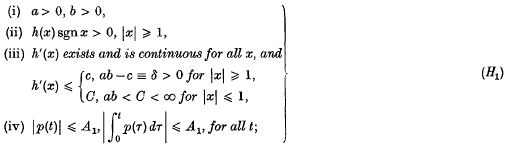
or, in the case (3),

In what follows here we shall refer to (2) and (H1) collectively as the (boundedness) hypotheses (BH1), and to (3) and (H2) as the hypotheses (BH2). Our object is to examine whether periodic solutions of (1) exist under the hypotheses (BH1), (BH2).

A recently developed theory of the electromagnetic field in nearly periodic structures is used to calculate the field in an Alvarez type linear accelerator. The problem is reduced to the solution of the transmission line equations for the ‘voltage’ and ‘current’ of the dominant mode. Formulae are given for the coefficients in these equations, and also for the ratio of mode current to accelerating field, as functions of the cavity dimensions of the accelerator; numerical values are given for the Berkeley accelerator.

The stability of the equilibrium solutions of the equations describing the behaviour of a system of coupled disk dynamos is investigated. In the absence of viscous damping, it is found that systems consisting of more than two dynamos are unstable. That a single disk dynamo is stable is known. The stability of the undamped two-dynamo system has not been ascertained. When viscous damping is present, there are two equilibrium solutions, one in which all the currents are zero, and one in which they are finite. In the zero-current case, a stability criterion is found. Stability criteria are also found in the finite-current case. Further, the existence of the finite-current equilibrium state excludes the stability of the zero-current equilibrium state.

In this paper explicit expressions in closed forms are first obtained for the complex potentials and deflexion at any point of a circular annular plate under various edge conditions when the plate is acted upon by general line loadings distributed along the circumference of a concentric circle. These solutions are then used to discuss the bending of a circular plate with a central hole under a concentrated load or a concentrated couple acting at any point of the plate. Solutions for singularly loaded sectorial plates bounded by two arcs of concentric circles and two radii are also derived when the plate is simply supported along the straight edges. The boundary conditions along the circular edges include the cases of a free boundary as well as the elastically restrained boundary which covers the usual rigidly clamped and simply supported boundaries as special cases. The usual restrictions relating to the small deflexion theory of thin plates of constant thickness are assumed. Limiting forms of the resulting solutions are investigated.

Two-dimensional elastic waves in a half-space 0 ≤ r < ∞, 0 ≤ θ ≤ π are examined under the assumption of dynamic similarity, so that the stresses depend only on r/t, θ. Analytic solutions are given for constant surface traction on θ = 0, 0 < r/t < V, where V is constant, the rest of the surface being unloaded, and for a concentrated load at r = 0.

Numerical results are quoted for the particular case V → ∞, corresponding to a load on half the bounding plane.

The radial charge densities tabulated opposite were communicated some years ago by the late D. R. Hartree to R. J. Weiss, of the Ordnance Materials Research Office, Watertown Arsenal, Watertown 72, Massachusetts, U.S.A. At his suggestion they are now published, no self-consistent field calculations for Ti being available. It is not known how Hartree obtained the wave functions which he describes as ‘estimated’, but it is presumed that they are interpolated. Radial charge densities for the 3d electrons for Ti+1 have already been published (l).

We consider a random walk on a two-dimensional rectangular lattice in which steps are strictly between nearest neighbour points. The conditions of the walk are that the walker must, at each step, turn either to the right or to the left of his previous step with respective probabilities ½(1+α), ½(1−α), (≤ α ≤ 1). To fix the ideas it is assumed that he starts from the origin and the probability of each of the four possible starting directions is ¼. If Ar denotes the probability of return to the origin after r steps we shall show that

where β = ½(α + α−1) and Pn is the nth Legendre polynomial. It is clear that Ar is zero for r ≢ 0(mod 4).

The notion of the order of convergence of iterative processes may well have been known to Gauss or even Newton, but to the author's knowledge it was first considered in detail in 1870 by Schröder(5). The subject was later investigated independently by Hartree(4) and Bodewig(1). Hartree alone mentions, briefly, the extension from one to several variables, but gives no detailed analysis. Domb and Fisher(2) consider a particular type of iterative process in several variables, which they call ‘degenerate’, in which all the variables tend to the same value. We shall follow essentially Hartree's treatment, in considering the solution of r simultaneous equations in r variables and applications to a generalization of the Newton-Raphson process.

The theorems of Pitman and Koopman on laws of chance that yield sufficient statistics are extended to laws where the parameter or the observable, or both, may admit only a discrete set of values. The method depends on making changes, not necessarily small, within the values permitted for the variables, but it is still necessary to assume a solubility condition.

There has lately been an unusual amount of interest in a relativistic phenomenon which has come to be called the clock paradox. It may be simply stated in the following way. If a man were to leave the earth on a powered space ship for an extended trip into space, he would find upon returning to earth that he was younger than he would have been if he had remained on earth.