Front matter
PSP volume 56 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Research Article
Non-linear Lagrangians and Palatine's device
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 396-400
-
- Article
- Export citation
Articles
The Fredholm Solution as the Limit for a Sum of Separable Potentials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 182-185
-
- Article
- Export citation
Research Article
An extension of the Newtonian law of gravitation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-409
-
- Article
- Export citation
Research Note
A Note on the Use of Logical Computers to Determine the most Efficient Method of using Factory Machines
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 186-188
-
- Article
- Export citation
Back matter
PSP volume 56 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Energy transfer by gravitation in Newtonian theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 410-413
-
- Article
- Export citation
Front matter
PSP volume 56 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 56 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Flexural problems of circular ring plates and sectorial plates. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 414-424
-
- Article
- Export citation
Research Note
On the 1-dimensional category of Cartesian products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 425-426
-
- Article
- Export citation
Proceedings at the meetings
Proceedings at the meetings held during the session 1959–1960
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 427-430
-
- Article
- Export citation
Front matter
PSP volume 56 issue 4 Cover, Front matter and Errata
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 56 issue 4 Cover, Back matter and Statement of Accounts
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b9
-
- Article
-
- You have access
- Export citation

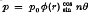 distributed over the entire circular ring plate. Solutions corresponding to the case φ(
distributed over the entire circular ring plate. Solutions corresponding to the case φ(

