A family ℳ of closed circular discs in the plane is called a saturated family or a saturated system of circles if (i) the infimum r of the radii of the discs in ℳ is positive and (ii) every closed disc of radius r in the plane intersects at least one disc in ℳ. For a saturated family ℳ, we denote by S the point-set union of the interiors of the members of ℳ and by S(l) the part of S inside the circular disc of radius l centred at the origin. We define the lower density ρℳ of the saturated family ℳ as

where V(S(l)) denotes the Lebesgue measure of the set S(l).

Segal(4) defines the algebra of measurable operators affiliated with a von Neumann algebra, and convergence nearly everywhere of a sequence of measurable operators, and shows that addition is jointly sequentially continuous and multiplication separately sequentially continuous in the star topology associated with convergence nearly everywhere.

Let ℛ be a von Neumann algebra, with predual ℛ*, acting on a Hilbert space ℋ; G a locally compact group with left Haar measure m, and α a representation of G on aut (ℛ), the group of all *-automorphisms of ℛ, i.e. α is a group homomorphism from G to aut (ℛ). We shall show that if ℋ is separable, then very weak measurability assumptions on the representation α produce strong continuity properties. This will be used to obtain results on the extension of representations from a C*-algebra to its weak closure, giving a much simpler proof of a result of Aarnes ((1), theorem 8, p. 31), and on continuity of tensor products of representations. The main result was suggested by the analogous theory concerning unitary representations of locally compact groups, and its proof employs ideas frequently used in that context. (See, for example, (5), theorem 22.20 (b), p. 347.)

Let (E, τ) be a complete, semi-metrizable topological vector space. Let p be a pseudo-norm (not to be confused with a semi-norm, cf. (8), p. 18) inducing the topology τ. For each positive real number r, let

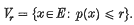
Let f be a continuous linear function from E into a topological vector space F. The open mapping theorem of Banach may be stated as follows: If f is nearly open, that is, if the closure 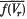of each f(Vr) is a neighbourhood of O in F then 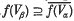whenever β > α > O; in particular, each f(Vr) is a neighbourhood of O. We note that f, identifying with its graph, is a closed linear subspace of the product space E × F. In this paper, we shall employ techniques developed by Kelley (6) and Baker (1) to extend the theorem to the case where f is taken to be a closed cone in E × F. The generalized theorem throws some light onto the duality theory of ordered spaces. In particular, the theorem of Andô–Ellis is generalized to (not assumed, a priori to be complete) normed vector spaces.

In this paper we derive the conditions which have to be satisfied in order to obtain some classes of zeros of the generalized hypergeometric series of the type

These conditions read:

Let F be the finite field of q = pn elements and let F0 be its prime subfield; thus, card F0 = p. For polynomials f ∈ F[x] and non-principal additive characters η of F A. Weil (1) proved the estimate

This result does not appear to be in the literature, though the method of proof is related to those used in (1) and, particularly, (2) to prove A. H. Stone's theorem that metrics have paracompact topologies.

Let X be a complex normed space and let T be a Hermitian linear operator on X (i.e. the numerical range of T is real). It was proved by Bonsall (see (4); Theorem 10.13) that then

for every u ∈ X. This inequality was improved by the author (3) to

Inequality (1) is closely related (see (3)) to some inequalities of Hadamard (6) and Kolmogorov (7) about the successive derivatives of functions in L∞(−∞, ∞). It was also shown in (3) (and was, in fact, shown already in (7)) that the constant 2 is best possible in (1). However, as we shall see, inequality (1) can be sharpened considerably if T attains its norm on u, i.e. if ‖Tu‖ = ‖T‖‖u‖.

The object of this paper is to complete the half proved theorem 2 of (1).

Let be a primitive fifth root of unity. Any element of Z[ζ] is a polynomial f(ζ) in ζ of degree ≤ 3 since 1 + ζ + ζ2 + ζ3 + ζ4 = 0. The units of Z[ζ] are ± ζi(1 + ζ)i or better still , with 0 ≤ i ≤ 4, j ε Z, where is the fundamental unit of the maximal real subfield of Q(ζ).

A necessary and sufficient condition for operator equations Tϕ = M(u, ϕ), T*u = N(u, ϕ) to arise from a variational principle is presented.

Suppose (en) is a basis of a Banach space E, and that (e′n) is the dual sequence in E′. Then if (e′n) is a basis of E′ in the norm topology (i.e. (en) is shrinking) it follows that E′ is norm separable: it is easy to give examples of spaces E for which this is not so. Therefore there are plenty of spaces which cannot have a shrinking basis. This leads one to consider whether it might not be reasonable to replace the norm topology on E′ by one which is always separable (provided E is separable). Of course, the weak*-topology σ(E′, E) is one possibility (Köthe (17), p. 259); then it is trivial that (e′n) is a weak*-basis of E′. However, if the weak*-topology is separable, then so is the Mackey topology τ(E′, E) on E′, and so we may ask whether (e′n) is a basis of (E′,τ(E′, E)).

It is shown that in the four-dimensional, source-free Einstein–Maxwell theory, four distinct orthogonal eigenvectors of the energy-momentum tensor may be obtained formally by the action of four projection operators on an almost arbitrary vector.

The extremal field, of the unified theory of Maxwell, Einstein and Rainich, is obtained explicitly in terms of eigenvectors of the energy-momentum tensor and the energy-momentum tensor itself, expressed in terms of eigenvectors, is seen to take on two equivalent forms. From this, a two-parameter group of Lorentz rotations, which leave the tetrad of eigenvectors unchanged, is deduced.

In many mechanical and other problems the following equation

is reached, where Jν(α) and Yν(α) are Bessel functions of the first and second kind of any real order ν and β is a positive parameter.

For example, equation (1) is reached in the case of determining the critical load Pcr, for a simply supported strut with a variable inertia moment by a power law, where the power m is any real number.

The asymptotic treatment of high-frequency scalar wave problems has in the past been rather unsatisfactory. Typically, the integral representations which arose were evaluated by stationary phase, or as a series of residues. The justification of these methods was usually heuristic and formal. In this paper, a method is advanced which, it is claimed, may be applied to any one-parameter separation of variables problem. The method assumes an integral representation whose contour of integration is the real axis. It is then only necessary to deform this contour in the neighbour-hood of the real axis to derive rigorous asymptotic expansions of the field in both the illumination and shadow. The method is applied to the particular example of scattering by a plane boundary in a general stratified medium with monotonically increasing refractive index.

In 1968, Amemiya and Kōmura ((1), p. 275) gave an example of a separable and incomplete Montel space. Their example depended upon constructing a subspace of ω, the countable product of real lines, which had several properties and in particular had codimension in ω. There is an error on page 276, line 5 of the proof of the Hilfssatz concerning this construction. The constructed subspace has codimension one. A more delicate construction is needed here; in fact, an example given by Webb ((7), p. 360) is sufficient to make this correction.

In this paper the authors consider a problem, frequently encountered in diffraction theory, of expanding a given function f(r) in terms of a set of orthogonal functions which is not complete. The expansion in question can be written as

where r < a and

In many contributions to the theory of Hausdorff measures, it has been the practice to place certain restrictions on the measure functions used. These restrictions usually ensure both the monotonicity and the continuity of the functions. The purpose of this work is to find conditions under which the restrictions of monotonicity and continuity may be relaxed. We shall be working mostly with sets in Euclidean space, although in the final theorem, we work in Hilbert space to show that some of our previous results do not generalize to this space. I am grateful to the referee for suggesting improvements in the proofs of the results.

This is the second part of a two-part paper in which a systematic method is advanced for treating separation of variables problems asymptotically as the frequency becomes large. The method assumes an integral representation in which the contour of integration is the real axis. The contour is then deformed in the neighbourhood of the real axis to derive rigorous asymptotic expansions of the field. In this paper the method is applied to scattering in homogeneous media by the circular and parabolic cylinders.

It is proved that the elliptic ball criterion is a necessary condition on the matrix M(t) for the linear feedback control equation f(D)x + BM(t)g(D)x = 0 to have a special kind of quadratic Lyapunov function. That it is also a sufficient condition has already been proved elsewhere. These two facts lead to a comparison theorem which enables the existence of a quadratic Lyapunov function for one equation to be deduced from that for another equation.

The to method of matched asymptotic expansions is employed to calculate the mass tre sport velocity due to combinations of small amplitude oscillatory waves propagatir, at a single frequency in fluid systems with density and viscosity dis-continuities. Interfacial boundary layers are considered in terms of the curvilinear coordinate system described by Longuet-Higgins(1). The order of magnitude of the mass transport velocity calculated for a general oscillatory disturbance is the same as that calculated for interfacial progressive waves by Dore(2). For standing waves, the time-averaged motion of the fluid particles forms a cellular structure in each fluid layer; the mass transport velocity due to modal interactions is associated with a similar structure.