Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T02:44:14.775Z Has data issue: false hasContentIssue false
  • English
  • Français

An open mapping theorem

Published online by Cambridge University Press:  24 October 2008

Kung-Fu Ng
Kung-Fu Ng
Affiliation:
United College, The Chinese University of Hong Kong
Get access Rights & Permissions [Opens in a new window]

Extract

Let (E, τ) be a complete, semi-metrizable topological vector space. Let p be a pseudo-norm (not to be confused with a semi-norm, cf. (8), p. 18) inducing the topology τ. For each positive real number r, let

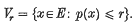
Let f be a continuous linear function from E into a topological vector space F. The open mapping theorem of Banach may be stated as follows: If f is nearly open, that is, if the closure 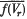of each f(Vr) is a neighbourhood of O in F then 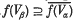whenever β > α > O; in particular, each f(Vr) is a neighbourhood of O. We note that f, identifying with its graph, is a closed linear subspace of the product space E × F. In this paper, we shall employ techniques developed by Kelley (6) and Baker (1) to extend the theorem to the case where f is taken to be a closed cone in E × F. The generalized theorem throws some light onto the duality theory of ordered spaces. In particular, the theorem of Andô–Ellis is generalized to (not assumed, a priori to be complete) normed vector spaces.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 74 , Issue 1 , July 1973 , pp. 61 - 66
Copyright
Copyright © Cambridge Philosophical Society 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baker, J. W.Continuity in ordered spaces. Math. Z. 104 (1968), 231–246.CrossRefGoogle Scholar
(2)Duhoux, M. Topologies semi-dirigées et éspaces vectoriels préordonnés (semi-)O-infratonneles, Séminaires de mathématique pure (Université Catholoqie de Louvain).Google Scholar
(3)Ellis, A. J.The duality of partially ordered normed linear spaces. J. London Math. Soc. 39 (1964), 730–744.CrossRefGoogle Scholar
(4)Husain, A. J.The open mapping and closed graph theorems in topological vector spaces (Oxford Mathematical monographs, 1965).CrossRefGoogle Scholar
(5)Jameson, G.Ordered linear spaces (Springer-Verlag lecture notes, 1970).CrossRefGoogle Scholar
(6)Kelley, J. L.General topology (New York, Van Nostrand, 1959).Google Scholar
(7)Ng, K.-F.Solid sets in ordered topological vector spaces. Proc. London Math. Soc. 22 (1971), 106–120.Google Scholar
(8)Schaefer, H. H.Topological vector spaces (New York: Macmillan, 1966).Google Scholar
(9)Wilansky, A.Functional analysis (New York: Blaisdell, 1964).Google Scholar