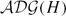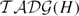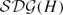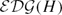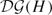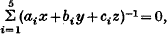Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 1
The injective tensor product of ℒp-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 237-242
-
- Article
- Export citation
- Cited by 1
Isometries of self-adjoint complex function spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 133-138
-
- Article
- Export citation
- Cited by 1
A Geometrical treatment of the Correspondence between Lines in Threefold Space and Points of a Quadric in Fivefold space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 694-699
-
- Article
- Export citation
- Cited by 1
Jacobians of linear systems on an algebraic variety
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 198-201
-
- Article
- Export citation
- Cited by 1
On certain sets of integers and intersectivity
-
- Published online by Cambridge University Press:
- 26 October 2001, pp. 157-164
-
- Article
- Export citation
- Cited by 1
An application of the Thue–Siegel–Roth theorem to elliptic functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 157-161
-
- Article
- Export citation
- Cited by 1
On direct decompositions. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-34
-
- Article
- Export citation
- Cited by 1
Analytic functions of finite dimensional linear transformations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 51-61
-
- Article
- Export citation
- Cited by 1
Inequivalent, bordant group actions on a surface
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 233-238
-
- Article
- Export citation
- Cited by 1
High-frequency diffraction of the radiation from a nearby source
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1145-1155
-
- Article
- Export citation
- Cited by 1
Analysis of tangential properties of curves of infinite length
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 69-72
-
- Article
- Export citation
- Cited by 1
Equivalent functions: hybrids and Wannier functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 197-206
-
- Article
- Export citation
- Cited by 1
The charge distribution and dipole moment of the C—H bond
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 509-510
-
- Article
- Export citation
- Cited by 1
Geometry of the augmented disk graph
-
- Published online by Cambridge University Press:
- 02 January 2014, pp. 363-382
-
- Article
- Export citation
- Cited by 1
Symmetrical treatment of a case of normal correlation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 107-109
-
- Article
- Export citation
- Cited by 1
Geometrical Properties of Three Symmetric Matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 174-182
-
- Article
- Export citation
- Cited by 1
On topological games
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 165-171
-
- Article
- Export citation
- Cited by 1
On the degrees of polynomial divisors over finite fields
-
- Published online by Cambridge University Press:
- 19 May 2016, pp. 469-487
-
- Article
- Export citation
- Cited by 1
The moment of the fluid forces acting on a plate which is gliding on the surface of a stream
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-184
-
- Article
- Export citation
- Cited by 1
Ergodic actions on nilmanifolds and restriction of unitary representations to lattices
-
- Published online by Cambridge University Press:
- 26 October 2001, pp. 91-96
-
- Article
- Export citation

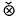
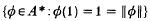
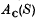 , and re
, and re 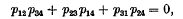
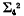 of four dimensions in five dimensional space,
of four dimensions in five dimensional space, 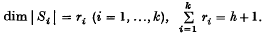
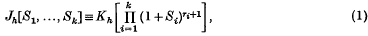
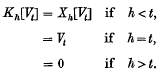
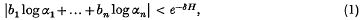
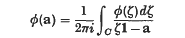
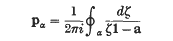
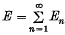 of sets of finite measure. Write
of sets of finite measure. Write