Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 1
On Mill's Ratio
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 363-364
-
- Article
- Export citation
- Cited by 1
On a problem of Steinhaus about polygons
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 686-688
-
- Article
- Export citation
- Cited by 1
Chief factors in Polish groups
- Part of:
-
- Published online by Cambridge University Press:
- 30 June 2021, pp. 239-296
-
- Article
- Export citation
- Cited by 1
A note on the representation of functions by absolutely convergent fourier integrals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 8-12
-
- Article
- Export citation
- Cited by 1
Continuity of homomorphisms of topological algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 171-172
-
- Article
- Export citation
- Cited by 1
Consistency and Nörlund means
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 107-109
-
- Article
- Export citation
- Cited by 1
Hadamard–Landau inequalities in uniformly convex spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 259-264
-
- Article
- Export citation
- Cited by 1
A Tauberian theorem for Borel summability
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-138
-
- Article
- Export citation
- Cited by 1
Semimartingales and the empirical distribution
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-171
-
- Article
- Export citation
- Cited by 1
Geometric limits of cyclic groups and the shape of Schottky space
-
- Published online by Cambridge University Press:
- 07 July 2004, pp. 55-68
-
- Article
- Export citation
- Cited by 1
Determination of a convex body from the average of projections and stability results
-
- Published online by Cambridge University Press:
- 01 May 1998, pp. 561-569
-
- Article
- Export citation
- Cited by 1
Regularity of induced representations and a theorem of Quigg and Spielberg
-
- Published online by Cambridge University Press:
- 30 September 2002, pp. 249-259
-
- Article
- Export citation
- Cited by 1
Harmonic measure on 3-dimensional Brownian paths
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 407-412
-
- Article
- Export citation
- Cited by 1
Tangents of σ-finite curves and scaled oscillation
-
- Published online by Cambridge University Press:
- 28 January 2016, pp. 1-12
-
- Article
- Export citation
- Cited by 1
The calculation of matrix elements of three particle operators in α-particle nuclei
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 457-458
-
- Article
- Export citation
- Cited by 1
A decomposition identity for a class of Riemannian invariants†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 459-463
-
- Article
- Export citation
- Cited by 1
Embeddings of real projective spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 555-557
-
- Article
- Export citation
- Cited by 1
A criterion for the (e, c)-summability of Fourier series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 121-127
-
- Article
- Export citation
- Cited by 1
Unbalanced quadratic residues and non-residues
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 9-17
-
- Article
- Export citation
- Cited by 1
Non-Relativistic Dispersion Relations for a Two Channel Scattering Process
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 363-376
-
- Article
- Export citation

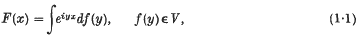
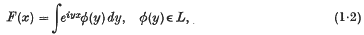


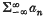 with partial sums {
with partial sums {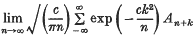
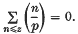




 is the Fourier transform of the potential
is the Fourier transform of the potential 
