Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 1
Locally compact topologies on abelian groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 233-235
-
- Article
- Export citation
- Cited by 1
On a heat flow problem in a hollow circular cylinder
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 193-202
-
- Article
- Export citation
- Cited by 1
An empirical form of the square root law and the central limit theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 287-295
-
- Article
- Export citation
- Cited by 1
Cohomology of groups and splendid equivalences of derived categories
-
- Published online by Cambridge University Press:
- 26 November 2001, pp. 459-472
-
- Article
- Export citation
- Cited by 1
The support of tempered distributions
-
- Published online by Cambridge University Press:
- 01 March 2008, pp. 495-498
-
- Article
- Export citation
- Cited by 1
A generalized Euler–Lagrange equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 399-401
-
- Article
- Export citation
- Cited by 1
Maximum-likelihood estimators with known incidental parameters
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 233-241
-
- Article
- Export citation
- Cited by 1
On the transverse circulation in streams
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 20-25
-
- Article
- Export citation
- Cited by 1
A note on the diamagnetism of free electrons
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 744-746
-
- Article
- Export citation
- Cited by 1
Demagnetizing coefficients and hysteresis losses of rectangular iron-silicon strips
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 254-261
-
- Article
- Export citation
- Cited by 1
Note on the multiplication of series by Cauchy's rule
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 251-252
-
- Article
- Export citation
- Cited by 1
Some infinite families in the stable homotopy of spheres
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 477-485
-
- Article
- Export citation
- Cited by 1
Chain recurrence in flows on the Klein bottle
-
- Published online by Cambridge University Press:
- 01 July 1999, pp. 83-91
-
- Article
- Export citation
- Cited by 1
A preliminary note on a direct determination of the distribution of intensity in the natural β-ray Spectrum of RaB and RaC
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 597-600
-
- Article
- Export citation
- Cited by 1
A note on lemmas of Green and Kondo
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 83-85
-
- Article
- Export citation
- Cited by 1
Triple points of unknotting discs and the Arf invariant of knots
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-129
-
- Article
- Export citation
- Cited by 1
Bundles of Grassmannians and integrality theorems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 45-53
-
- Article
- Export citation
- Cited by 1
ℤ2-equivariant hierarchies of irreducible 3-manifolds containing two-sided projective planes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-125
-
- Article
- Export citation
- Cited by 1
Summability fields which span the bounded sequences
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-106
-
- Article
- Export citation
- Cited by 1
On Riesz logarithmic summability of the ultraspherical series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-170
-
- Article
- Export citation

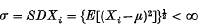
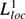 and be of polynomial growth. We use an apparently new technical lemma that implies that certain bounded approximate identities for
and be of polynomial growth. We use an apparently new technical lemma that implies that certain bounded approximate identities for 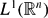 are also topological approximate identities for elements of the space
are also topological approximate identities for elements of the space 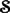 of Schwartz functions.
of Schwartz functions.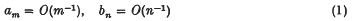
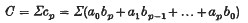

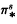 . In this paper we make another contribution to this computation.
. In this paper we make another contribution to this computation.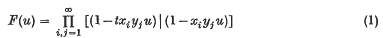
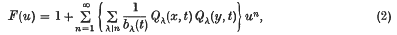
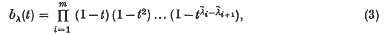
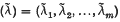 is the partition of
is the partition of 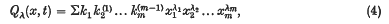
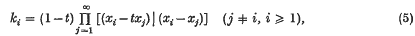
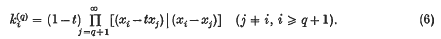
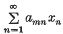 and
and 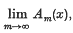 if that limit exists. We shall denote by
if that limit exists. We shall denote by 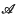 the set of bounded sequences which are summed by
the set of bounded sequences which are summed by 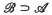 then we say that
then we say that 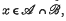 then
then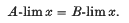
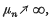 we say that
we say that 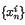 is summed by
is summed by 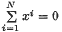 implies that
implies that 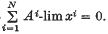 The set of sequences,
The set of sequences, 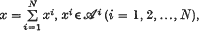 is denoted by
is denoted by 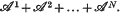
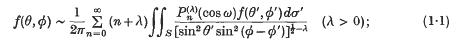
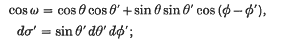
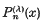 are defined by the following expansion
are defined by the following expansion