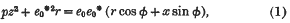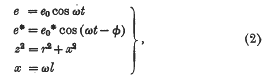Research Article
Explicit formulae connecting Hölder's, Cesàro's and another mean value
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-17
-
- Article
- Export citation
Some enumerative results for curves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 18-22
-
- Article
- Export citation
The application of quadratic forms in an infinity of variables to boundary problems in partial differential equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-34
-
- Article
- Export citation
Note on the instability of a surface of discontinuity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 35-44
-
- Article
- Export citation
The tangent planes to a degenerate surface
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 45-50
-
- Article
- Export citation
The general surfaces in four dimensions with one or two apparent triple points
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 51-54
-
- Article
- Export citation
A note on inverse probability
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 55-61
-
- Article
- Export citation
Note in regard to surfaces in space of four dimensions, in particular rational surfaces*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 62-82
-
- Article
- Export citation
The ‘relaxation’ term in Debye and Hückel's theory of ionic mobility
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 83-92
-
- Article
- Export citation
A condensation diagram
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 93-98
-
- Article
- Export citation
The collision of electrons with rotating dipoles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-105
-
- Article
- Export citation
Note on a new power-angle diagram for alternators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 106-108
-
- Article
- Export citation
On the determination of the horizontal component of the earth's magnetic field by a coupled oscillations method
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-114
-
- Article
- Export citation
The upper limit of energy in the β-ray spectrum of thorium C″
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 115-120
-
- Article
- Export citation
Note on a high-tension supply for Geiger counters operated from A.C. mains
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 121-123
-
- Article
- Export citation
An attempt to detect the spontaneous transformation of helium into penetrating radiation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 124-127
-
- Article
- Export citation
The interval between the departure of the disintegration particle and the emission of the gamma radiation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 128-135
-
- Article
- Export citation
A quantum mechanical theory of energy exchanges between inert gas atoms and a solid surface
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 136-164
-
- Article
- Export citation
Front matter
PSP volume 28 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 28 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

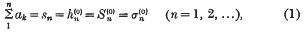
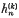 are defined by
are defined by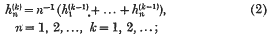
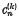 are defined by
are defined by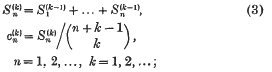
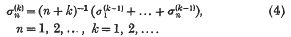
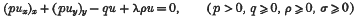
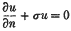 on Γ, the boundary of
on Γ, the boundary of 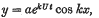
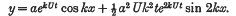
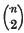 double lines, and in threes, forming
double lines, and in threes, forming 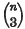 triple points. The tangent cone to φ from an arbitrary point consists of
triple points. The tangent cone to φ from an arbitrary point consists of