Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T01:36:50.438Z Has data issue: false hasContentIssue false
  • English
  • Français

The application of quadratic forms in an infinity of variables to boundary problems in partial differential equations

Published online by Cambridge University Press:  24 October 2008

S. W. P. Steen
S. W. P. Steen
Affiliation:
Christ's College
Get access Rights & Permissions [Opens in a new window]

Extract

The object of this paper is to find the characteristic functions and the characteristic numbers of the partial differential equation

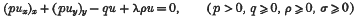
valid in a domain G, and where 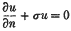on Γ, the boundary of G. The method employed is to transform two quadratic forms to their common self-conjugate “triangle“ of reference. The solution to the problem is given by this method in a simple manner, without the use of the integral equation theory, or the use of minimal sequences.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 28 , Issue 1 , January 1932 , pp. 23 - 34
Copyright
Copyright © Cambridge Philosophical Society 1932

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Courant-Hilbert, , Methoden der mathematischen Physik, Ch. 6.Google Scholar

† The method of this paragraph is obtained from Hilbert, , Grundzüge einer allgemeine Theorie der linearen Integralgleichungen, pp. 147et seq.Google Scholar

* When , hence |x i| < √K.

* By this we mean that every point of C 1′ is at an equal distance δ from C 1, and that C 1′ has no double points.

* Courant-Hilbert, loc. cit., Ch. 6, p. 328.