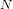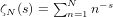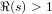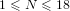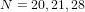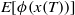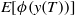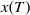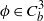Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 2
p-adic class invariants
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2011, pp. 108-126
-
- Article
-
- You have access
- Export citation
- Cited by 2
The linear programming relaxation permutation symmetry group of an orthogonal array defining integer linear program
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2016, pp. 206-216
-
- Article
-
- You have access
- Export citation
- Cited by 2
A Domain-Theoretic Approach to Integration in Hausdorff Spaces
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 229-273
-
- Article
-
- You have access
- Export citation
- Cited by 2
Improved Bounds for the Spread of Sporadic Groups
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 132-140
-
- Article
-
- You have access
- Export citation
- Cited by 2
An Algorithm for Recognising the Exterior Square of a Multiset
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 96-116
-
- Article
-
- You have access
- Export citation
- Cited by 2
Three-Dimensional Presentations for the Groups of Order at Most 30
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 93-117
-
- Article
-
- You have access
- Export citation
- Cited by 2
Strong Spatial Mixing and Rapid Mixing with Five Colours for the Kagome Lattice
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 195-227
-
- Article
-
- You have access
- Export citation
- Cited by 2
Primitive Divisors on Twists of Fermat's Cubic
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 54-81
-
- Article
-
- You have access
- Export citation
- Cited by 2
An Algorithmic Analysis of the Intersection Property
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 284-299
-
- Article
-
- You have access
- Export citation
- Cited by 2
Computing Borcherds products
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2013, pp. 200-215
-
- Article
-
- You have access
- Export citation
- Cited by 2
Ergo 6: A Generic Proof Engine that Uses Prolog Proof Technology
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 194-219
-
- Article
-
- You have access
- Export citation
- Cited by 2
A comprehensive perturbation theorem for estimating magnitudes of roots of polynomials
-
- Published online by Cambridge University Press:
- 14 February 2013, pp. 1-8
-
- Article
-
- You have access
- Export citation
- Cited by 2
Automorphisms of hyperelliptic modular curves X0(N) in positive characteristic
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2010, pp. 144-163
-
- Article
-
- You have access
- Export citation
- Cited by 2
Zeroes of partial sums of the zeta-function
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2016, pp. 37-41
-
- Article
-
- You have access
- Export citation
- Cited by 1
An Algorithm to Compute the Canonical Basis of an Irreducible Module Over a Quantized Enveloping Algebra
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 105-118
-
- Article
-
- You have access
- Export citation
- Cited by 1
The character table of a group of shape (2×2.G):2
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2010, pp. 82-89
-
- Article
-
- You have access
- Export citation
- Cited by 1
Effective Hasse principle for the intersection of two quadrics
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2016, pp. 73-82
-
- Article
-
- You have access
- Export citation
- Cited by 1
The Chamber Graph of the M24 Maximal 2-Local Geometry
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 120-143
-
- Article
-
- You have access
- Export citation
- Cited by 1
A Priori Estimates for the Global Error Committed by Runge-Kutta Methods for a Nonlinear Oscillator
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 18-28
-
- Article
-
- You have access
- Export citation
- Cited by 1
Weak approximation of stochastic differential delay equations for bounded measurable function
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2013, pp. 319-343
-
- Article
-
- You have access
- Export citation

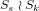

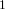
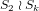



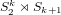
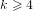

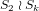
 of a modular curve
of a modular curve