Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T20:56:16.728Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphisms of hyperelliptic modular curves X0(N) in positive characteristic

Part of: Curves Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  01 April 2010

Aristides Kontogeorgis  and
Yifan Yang
Aristides Kontogeorgis
Affiliation:
Max-Planck-Institut für Mathematik Vivatsgasse 7, 53111 Bonn, Germany Department of Mathematics, University of the Aegean, 83200 Samos, Greece (email: [email protected])http://myria.math.aegean.gr/∼kontogar
Yifan Yang
Affiliation:
Max-Planck-Institut für Mathematik Vivatsgasse 7, 53111 Bonn, Germany Department of Applied Mathematics, National Chiao Tung University, Hsinchu 300, Taiwan (email: [email protected])

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the automorphism groups of the reduction 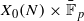of a modular curve X0(N) over primes p∤N.

MSC classification

Secondary: 14H37: Automorphisms 11F11: Holomorphic modular forms of integral weight 11G20: Curves over finite and local fields
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 13 , January 2010 , pp. 144 - 163
Copyright
Copyright © London Mathematical Society 2010

References

[1] Adler, A., ‘The Mathieu group M 11 and the modular curve X(11)’, Proc. Lond. Math. Soc. (3) 74 (1997) 1–28; MR 1416724 (97k:14021).CrossRefGoogle Scholar
[2] Atkin, A. O. L. and Lehner, J., ‘Hecke operators on Γ0(m)’, Math. Ann. 185 (1970) 134–160; MR 0268123 (42 #3022).CrossRefGoogle Scholar
[3] Bending, P., Camina, A. and Guralnick, R., ‘Automorphisms of the modular curve’, Progress in Galois theory, Developments in Mathematics 12 (Springer, New York, 2005) 25–37; MR 2148458 (2006c:14050).Google Scholar
[4] Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I: The user language’, J. Symbolic Comput. 24 (1997) 235–265.Google Scholar
[5] Brandt, R. and Stichtenoth, H., ‘Die Automorphismengruppen hyperelliptischer Kurven’, Manuscripta Math. 55 (1986) 83–92; MR 828412 (87m:14033).Google Scholar
[6] Chinburg, T., ‘Minimal models of curves over Dedekind rings’, Arithmetic geometry (eds Cornell, G. and Silverman, J.; Springer, New York, 1986) 309–326.Google Scholar
[7] Deligne, P. and Mumford, D., ‘The irreducibility of the space of curves of given genus’, Publ. Math. Inst. Hautes Études Sci. 36 (1969) 75–109; MR 0262240 (41 #6850).Google Scholar
[8] Elkies, N. D., ‘The automorphism group of the modular curve X 0(63)’, Compositio Math. 74 (1990) 203–208; MR 1047740 (91e:11064).Google Scholar
[9] Galbraith, S., ‘Equations for modular curves’, PhD Thesis, St. Cross College Mathematical Institute, Oxford, 1996.Google Scholar
[10] Glenn, O. E., ‘A treatise on the theory of invariants’, Project Gutenberg, http://www.gutenberg.org/etext/9933.Google Scholar
[11] Gonzàlez Rovira, J., ‘Equations of hyperelliptic modular curves’, Ann. Inst. Fourier (Grenoble) 41 (1991) 779–795; MR 1150566 (93g:11064).Google Scholar
[12] Green, D. J., ‘Cohomology rings of some small p-groups’, http://users.minet.uni-jena.de/cohomology/.Google Scholar
[13] Gutierrez, J., Sevilla, D. and Shaska, T., ‘Hyperelliptic curves of genus 3 with prescribed automorphism group’, Computational aspects of algebraic curves, Lecture Notes Series in Computing 13 (World Scientific, Hackensack, NJ, 2005) 109–123; MR 2182037 (2006j:14038).Google Scholar
[14] Gutierrez, J. and Shaska, T., ‘Hyperelliptic curves with extra involutions’, LMS J. Comput. Math 8 (2005) 102–115 (electronic); MR 2135032 (2006b:14049).Google Scholar
[15] Igusa, J.-I., ‘Kroneckerian model of fields of elliptic modular functions’, Amer. J. Math. 81 (1959) 561–577; MR 0108498 (21 #7214).Google Scholar
[16] Kenku, M. A. and Momose, F., ‘Automorphism groups of the modular curves X 0(N)’, Compositio Math. 65 (1988) 51–80; MR 930147 (88m:14015).Google Scholar
[17] Kontogeorgis, A., ‘The group of automorphisms of cyclic extensions of rational function fields’, J. Algebra 216 (1999) 665–706; MR 1692965 (2000f:12005).Google Scholar
[18] Kontogeorgis, A., ‘The group of automorphisms of the function fields of the curve xn+ym+1=0’, J. Number Theory 72 (1998) 110–136; MR 1643304 (99f:11074).Google Scholar
[19] Leopoldt, H.-W., ‘Über die Automorphismengruppe des Fermatkörpers’, J. Number Theory 56 (1996) 256–282; MR 1373551 (96k:11079).Google Scholar
[20] Lichtenbaum, S., ‘Curves over discrete valuation rings’, Amer. J. Math. 90 (1968) 380–403.Google Scholar
[21] Lockhart, P., ‘On the discriminant of a hyperelliptic curve’, Trans. Amer. Math. Soc. 342 (1994) 729–752; MR 1195511 (94f:11054).Google Scholar
[22] Ogg, A. P., ‘Über die Automorphismengruppe von X 0(N)’, Math. Ann. 228 (1977) 279–292; MR 0562500 (58 #27775).Google Scholar
[23] Ogg, A. P., ‘Hyperelliptic modular curves’, Bull. Soc. Math. France 102 (1974) 449–462; MR 0364259 (51 #514).Google Scholar
[24] Rajan, C. S., ‘Automorphisms of X(11) over characteristic 3 and the Mathieu group M 11’, J. Ramanujan Math. Soc. 13 (1998) 63–72; MR 1626720 (99f:14027).Google Scholar
[25] Ritzenthaler, C., ‘Automorphismes des courbes modulaires X(n) en caractéristique p’, Manuscripta Math. 109 (2002) 49–62; MR 1931207 (2003g:11067).CrossRefGoogle Scholar
[26] Sekiguchi, T. and Suwa, N., ‘Théories de Kummer–Artin–Schreier–Witt’, C. R. Acad. Sci. Paris Sér. I Math. 319 (1994) 105–110; MR 1288386.Google Scholar
[27] Sekiguchi, T. and Suwa, N., ‘Théorie de Kummer–Artin–Schreier et applications’, J. Théor. Nombres Bordeaux 7 (1995) 177–189; Les Dix-huitièmes Journées Arithmétiques (Bordeaux, 1993); MR 1413576 (98d:11139).Google Scholar
[28] Shaska, T., ‘Computational aspects of hyperelliptic curves’, Computer mathematics, Lecture Notes Series in Computing 10 (World Scientific, River Edge, NJ, 2003) 248–257; MR 2061839 (2005h:14073).Google Scholar
[29] Shaska, T., ‘Determining the automorphism group of a hyperelliptic curve’, Proceedings of the 2003 International Symposium on Symbolic and Algebraic Computation (ACM, New York, 2003) 248–254 (electronic); MR 2035219 (2005c:14037).Google Scholar
[30] Shaska, T. and Völklein, H., ‘Elliptic subfields and automorphisms of genus 2 function fields’, Algebra, arithmetic and geometry with applications, West Lafayette, IN, 2000 (Springer, Berlin, 2004) 703–723; MR 2037120 (2004m:14047).Google Scholar
[31] Shimura, M., ‘Defining equations of modular curves X 0(N)’, Tokyo J. Math. 18 (1995) 443–456; MR 1363479 (96j:11085).Google Scholar
[32] Tzermias, P., ‘The group of automorphisms of the Fermat curve’, J. Number Theory 53 (1995) 173–178; MR 1344839 (96e:11084).CrossRefGoogle Scholar
[33] Valentini, R. C. and Madan, M. L., ‘A Hauptsatz of L. E. Dickson and Artin–Schreier extensions’, J. Reine Angew. Math. 318 (1980) 156–177; MR 579390 (82e:12030).Google Scholar
[34] Weiss, E., Cohomology of groups, Pure and Applied Mathematics 34 (Academic Press, New York, 1969) MR 0263900 (41 #8499).Google Scholar