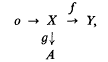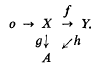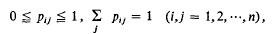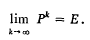Research Article
Formal multiplication of trigonometric series
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 70-77
-
- Article
-
- You have access
- Export citation
A lattice analogue of a theorem of Chow
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 216-219
-
- Article
-
- You have access
- Export citation
One-relater groups with center
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 319-323
-
- Article
-
- You have access
- Export citation
Index
Index to Volume XVI
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 511-512
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 16 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Varieties of topological groups and left adjoint functors
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 220-227
-
- Article
-
- You have access
- Export citation
The subnormal coalescence of some classes of groups of finite rank
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 324-327
-
- Article
-
- You have access
- Export citation
On minimal irregular p-Groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 78-89
-
- Article
-
- You have access
- Export citation
Oriented Tait graphs
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 328-331
-
- Article
-
- You have access
- Export citation
Permutable subgroups of some finite p-groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-97
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 16 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Annihilators of relation modules
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 228-233
-
- Article
-
- You have access
- Export citation
Subgroups of finitely presented metabelian groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 98-110
-
- Article
-
- You have access
- Export citation
The existence of Fano subplanes in generalized Hall planes
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 234-238
-
- Article
-
- You have access
- Export citation
Some small aspherical spaces
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 332-352
-
- Article
-
- You have access
- Export citation
Alternating trilinear forms and groups of exponent 6
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 111-128
-
- Article
-
- You have access
- Export citation
On finitely injective modules
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 239-248
-
- Article
-
- You have access
- Export citation
On the latent roots of a doubly stochastic matrix
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 353-356
-
- Article
-
- You have access
- Export citation
On one relator groups and HNN extensions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-256
-
- Article
-
- You have access
- Export citation
The nilpotent length of finite soluble groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-362
-
- Article
-
- You have access
- Export citation

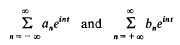
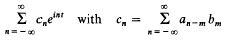
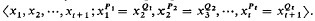 A necessary and a sufficient condition for the sequence (
A necessary and a sufficient condition for the sequence (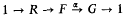 be a non-cyclic free presentation of a group
be a non-cyclic free presentation of a group 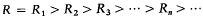 the lower central series of
the lower central series of