Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T08:53:27.405Z Has data issue: false hasContentIssue false
  • English
  • Français

On finitely injective modules

Published online by Cambridge University Press:  09 April 2009

V. S. Ramamurthi  and
K. M. Rangaswamy
V. S. Ramamurthi
Affiliation:
De La Salle College Karumathoor, Madurai Tamil Nadu, India
K. M. Rangaswamy
Affiliation:
Institute of Advanced Studies The Australian National UniversityCanberra, A. C. T. 2600, Australia.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

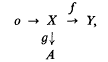A right module A over a ring R is called finitely injective if every diagram of right R-modules of the form where X is finitely generated and the row is exact, can be imbedded in a commutative diagram 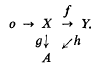The finitely injective modules turn out to have the nice property of being ‘strongly pure’ in all the containing modules and, in particular, are absolutely pure in the sense of Maddox [8]. For this reason we call them strongly absolutely pure (for short, SAP) modules. Several other characterizations of the SAP modules are obtained. It is shown that every module admits a ‘SAP hull’. The concepts of finitely M-injective and finitely quasi-injective modules are then investigated. A subclass of finitely quasi-injective modules, called the strongly regular modules, is studied in some detail and it is shown that, if R/J is right Noetherian, then the strongly regular right R-modules coincide with the semi-simple R-modules.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 16 , Issue 2 , September 1973 , pp. 239 - 248
Copyright
Copyright © Australian Mathematical Society 1973

References

[1]Azumaya, G., ‘M-projective and M-injective modules’, (unpublished).Google Scholar
[2]Chase, S. U., ‘Direct products of modules’, Trans. Amer. Math. Soc. 97 (1960), 457–473.CrossRefGoogle Scholar
[3]Cohn, P. M., ‘On the free product of associative rings’, Math. Z. 71 (1959), 380–398.CrossRefGoogle Scholar
[4]Fieldhouse, D. J., Regular modules and rings, (Queen's Univ., Preprint 1967).Google Scholar
[5]Fuchs, L., ‘On quasi-injective modules’, Ann. Scuola. Norm. Sup. Pisa (3) 23 (1969), 541–546.Google Scholar
[6]Kaplansky, I., ‘Projective Modules’, Ann. of Math. 68 (1958), 372–377.CrossRefGoogle Scholar
[7]Janakiraman, S., Ph. D. thesis, Madurai Univ. (1970).Google Scholar
[8]Maddox, B.H., ‘Absolutely pure modules’, Proc. Amer. Math. Soc. 18 (1967), 155–158.CrossRefGoogle Scholar
[9]Megibben, C., ‘Absolutely pure modules’, Proc. Amer. Math. Soc. 26 (1970), 561–566.CrossRefGoogle Scholar
[10]Osofsky, B.L., ‘Noninjective cyclic modules’, Proc. Amer. Math. Soc. 19 (1968), 1383–1384.CrossRefGoogle Scholar
[11]Ware, R., ‘Endomorphism rings of projective modules’, Trans. Amer. Math. Soc. 155 (1971), 233–256.CrossRefGoogle Scholar