This paper is concerned with two mani problems:

(a) the determination of the conjugacy classes in the finite-dimensional unitary, symplectic and orthogonal groups over division rings or fields;

(b) the determination of the equivalence classes of non-degenerate sesquilinear forms on finite-dimensional vector spaces.

Let G be a finite group. If N denotes a normal subgroup of G, a subgroup S of G is called a supplement of N if we have G = SN. For every normal subgroup of G there is always the trivial supplement S = G. The existence of a non-trivial supplement is important for the extension theory, i.e., for the description of G by means of N and the factor group G/N. Generally, a supplement S is the more useful the smaller the intersection S ∩ N. If we have even S ∩ N = 1, then S is called a complement for N in G. In this case G is a splitting extension of N by S.

A tetrad of Möbius tetrahedra consists of a set of 4 mutually inscribed and therefore circumscribed tetrahedra whose 16 vertices and 16 faces form a Kummer's 166 configuration (5; 11; 12; 21). As pointed out by the refere, fundamental to all work on the 166 figure are the 10 quadrics, called fundamental for the associated Kummer's quartic surface (13). To every quadric F correspond a matrix scheme of the 16 points or planes, arranged in 4 rows or columns, such that the 8 Rosenhain tetrahedra (7) formed of the rows and columns are all self-polar for F. The rows form one and the columns another tetrad of Mobius tetrahedra. Nine new schemes can be derived from one such scheme to make the total ten as explained by Baker (3, p. 133) leading to 80 Rosenhain tetrahedra in all. The 16 nodes (5; 8) or tropes of the Rummer's quartic are the 16 common elements of the 10 schemes such that the nodes and tropes are poles and polars for any one of the 10 quadrics. Each trope touches the quartic along a singular conic through the 6 points of the figure lying therein. The lines tangent to the surface at its each node N generate a quadric cone which is enveloped by the 6 tropes through N (12).

When a semi-infinite line load moves lengthways, at supersonic velocity, on the plane surface of an elastic solid, the resulting velocity field is conical. There are two characteristic cones, one associated with dilatation effects and the other with shear effects. The propagation process is more complicated than the well-known case of conical flow in supersonic aerodynamics not only because of the presence of two cones of discontinuity but also because the presence of a free surface implies interaction between shear and dilatation effects. It is the interaction process at the free surface which is examined in detail in this paper.

The results of this fundamental problem may be extended by the process of superposition to more general steadily moving loads. In particular by differentiating with respect to time, the potential of a steadily moving point load is obtained explicitly.

Milne-Thomson has used the method of analytic continuation to solve boundary value problems of the annulus in plane elastostatics. However, his use of Cauchy integrals is incorrect, and it is shown in this note that the solution is obtained in terms of Laurent Series expansions. The solution is equivalent to that of Muskhelishvili, but is simpler to use in some applications.

A similar approach is used to solve the boundary value problem of the infinite strip, the solution being given in terms of functions of a complex variable expressed as Fourier integrals.

It is known that various cases of the steady isentropic irrotational motion of a compressible fluid are expressible as variational principle [1], [5]. in particular, the aerofoil problem i.e. the case of plane flow in which a uniform stream is locally deflected, without circulation, by a bounded obstacle, can be expressed in such a form. Thus we make stationary where the region R is that bounded internally by the obstacle (C0) and externally by a circle (CR) of radius R. In this expression φ∞ is the velocity potential for a uniform stream, and φ0 is the velocity potential for the corresponding incompressible flow.

The random processes discussed here may be specified in the following way. A fixed population of N members is spilt into two distinct classes. Individuals move about randomly between the classes, and we are interested in the size of each class at any time, rather than in the behaviour of particular individuals. Let i(t) and N —i(t) be the numbers present in the repective classes at the time t. It is assumed that the process {i(t), t ≧ 0} is Markovian, and that transitions between the states j = 0, 1, … N, occur according to the conditional probabilities; and.

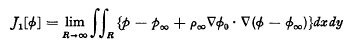
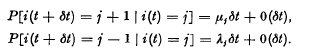
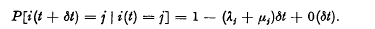
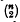When n objects are to be compared in pairs, a complete experiment requires N= comparisons. There are frequent occasions when it si desirable to make only a fraction F of the possible comparison, either because N is large or because even an individual comparison is laborious. The problem of what constitutes a satisfactory subset of the comparisons has been considered by Kendall [5[ who lays down the following two minimum requirements: (a) every object should appear equally often; (b) the design should be ‘connected‘ so that it is impossible to split the objects into two sets with no comparison made between objects in one set and objects in the other.