Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T09:12:46.014Z Has data issue: false hasContentIssue false
  • English
  • Français

The structure of cyclic paired-comparison designs

Published online by Cambridge University Press:  09 April 2009

H. A. David
H. A. David
Affiliation:
Virginia Polytechnic Insititute, Blackburg, Virginia, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

When n objects are to be compared in pairs, a complete experiment requires N= 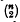comparisons. There are frequent occasions when it si desirable to make only a fraction F of the possible comparison, either because N is large or because even an individual comparison is laborious. The problem of what constitutes a satisfactory subset of the comparisons has been considered by Kendall [5[ who lays down the following two minimum requirements: (a) every object should appear equally often; (b) the design should be ‘connected‘ so that it is impossible to split the objects into two sets with no comparison made between objects in one set and objects in the other.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 3 , Issue 1 , February 1963 , pp. 117 - 127
Copyright
Copyright © Australian Mathematical Society 1963

References

[1]Clatworthy, W. H. (1995), Partially balanced incomplete block designs with two associate classes and two treatments per block. J. Bes., Nat. Stand. 54, 177–190.CrossRefGoogle Scholar
[2]David, H. A., The Method of Paired Comparisons. London: Griffin (In Press).Google Scholar
[3]Dickson, L. E., (1929)., Introduction to the Theory of Numbers. Chicago: Univeristy Press.Google Scholar
[4]Kempthorne, O. (1953), A class of experimental designs using blocks of two plots. Ann. Math. Statist. 24, 76–84.CrossRefGoogle Scholar
[5]Kendall, M. G. (1935), Further contributions to the theory of paired comparisons. Biometrics, 11, 43–62.CrossRefGoogle Scholar
[6]McKeon, J. J. (1960), Some eyclical incomplete paried comparisons designs. Tech. Rep. No. 24, Psychom. Lab., Univ. of North Carolina.Google Scholar
[7]Uspensky, J. V. and Heaslet, M. A. (1939), Elementary Number Theory. New York: MCGraw-Hill.Google Scholar