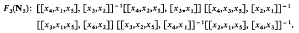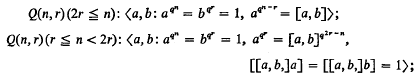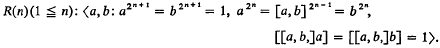Research Article
The laws of some nilpotent groups of small rank
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-132
-
- Article
-
- You have access
- Export citation
Growth sequences of finite groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 133-141
-
- Article
-
- You have access
- Export citation
Odd order nilpotent groups of class two with cyclic centre
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 142-153
-
- Article
-
- You have access
- Export citation
Formulae for well formed formulae and their enumeration
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 154-162
-
- Article
-
- You have access
- Export citation
Varieties and simple groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 163-173
-
- Article
-
- You have access
- Export citation
Direct products and the Hopf property
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 174-196
-
- Article
-
- You have access
- Export citation
Walking around the Brauer tree
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 197-213
-
- Article
-
- You have access
- Export citation
Poincare's conjecture and the homeotopy group of a closed, orientable 2-manifold
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 214-221
-
- Article
-
- You have access
- Export citation
Generating groups of certain soluble varieties
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 222-233
-
- Article
-
- You have access
- Export citation
Free products of hopfian lattices
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 234-245
-
- Article
-
- You have access
- Export citation
Some finitely based varieties of rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 246-255
-
- Article
-
- You have access
- Export citation
Corrigendum
Corrigendum
-
- Published online by Cambridge University Press:
- 09 April 2009, p. 256
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 17 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 17 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation