Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T09:01:48.228Z Has data issue: false hasContentIssue false
  • English
  • Français

Odd order nilpotent groups of class two with cyclic centre

Published online by Cambridge University Press:  09 April 2009

Y. K. Leong
Y. K. Leong
Affiliation:
Australian National University, Canberra, A. C. T. 2600
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The isomorphism problem for finite groups of odd order and nilpotency class 2 with cyclic centre will be solved using some results of Brady [1], [2]. Since a finite nilpotent group is the direct product of its Sylow subgroups, we only need to consider finite q-groups where q is a prime. It has been shown in [1] and [2] that a finite q-group of nilpotency class 2 with cyclic centre is a central product either of two-generator subgroups with cyclic centre or of two-generator subgroups with cyclic centre and a cyclic subgroup, and that the q-groups of class 2 on two generators with cyclic centre comprise the following list: 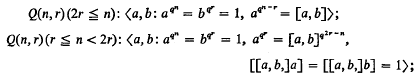, and if q = 2 we have as well .

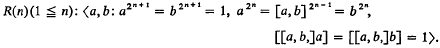Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 17 , Issue 2 , March 1974 , pp. 142 - 153
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Brady, J. M., Just-non-Cross varieties of groups (Ph. D. Thesis, Australian National University, 1970).CrossRefGoogle Scholar
[2]Brady, J. M., Bryce, R. A. and Cossey, John, ‘On certain abelian-by-nilpotent varieties’, Bull. Austral. Math. Soc. 1 (1969), 403–416.CrossRefGoogle Scholar
[3]Neumann, B. H., Lectures on topics in the theory of infinite groups (Tata Institute of Fundamental Research, Bombay, 1960).Google Scholar
[4]Newman, M. F., ‘On a class of nilpotent groups’, Proc. London Math. Soc. (3) 10 (1960), 365–375.CrossRefGoogle Scholar
[5] Marlene Schick, ‘On central decompositions of groups I, II’, (to appear).Google Scholar
[6]Tang, C. Y., ‘On uniqueness of central decompositions of groups’, Pacific J. Math. 33 (1970), 749–761.CrossRefGoogle Scholar