Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T09:13:31.638Z Has data issue: false hasContentIssue false
  • English
  • Français

The laws of some nilpotent groups of small rank

Published online by Cambridge University Press:  09 April 2009

T. C. Chau
T. C. Chau
Affiliation:
Department of Mathematics, Laurentian University, Sudbury, Ontario, Canada.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We shall take for granted the basic terminology currently in use in the theory of varieties of groups. Kovács, Newman, Pentony [2] and Levin [3] prove that if m is an integer greater than 2, then the variety Νm of all nilpotent groups of class at most m is generated by its free group Fm-1(Νm) of rank m – 1 but not by its free group Fm–2(Νm) of rank m — 2. That is, the free groups Fk(Nm), 2≦k ≦ m – 2, do not generate Nm. In general little is known of the varieties generated by them. The purpose of the present paper is to record the varieties of the free groups Fk(Nm) of the nilpotent varieties Nm of all nilpotent groups of class at most m for 2 ≦ k ≦ m – 2 and 5 ≦ m ≦ 6. This is done by describing a basis for the laws in these groups, that is a set of laws the fully invariant closure of which is the set of all laws for Fk(Nm). The set of laws, which, together with the appropriate nilpotency law, form a basis for the relevant groups Fk(Nm) are listed below: .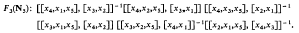

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 17 , Issue 2 , March 1974 , pp. 129 - 132
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Higman, Graham, ‘Representations of general linear groups and varieties of p-groups’, Proc. Internat. Conf. Theory of Groups, Austral. Nat. University, Canberra, August, 1965.Google Scholar
[2]Kovács, L. G., Newman, M. F., Pentony, P. F., ‘Generating groups of nilpotent varieties’, Bull. Amer. Math. Soc., 74 (1968), 968–971.CrossRefGoogle Scholar
[3]Levin, Frank, ‘Generating groups for nilpotent varieties’, Jour. Austral. Math. Soc., 11 (1970), 28–32.CrossRefGoogle Scholar
[4]Neumann, Hanna, Varieties of groups, Ergebinsse der Mathematik und ihrer Genezgebite Bd. 37. (Springer), 1967.CrossRefGoogle Scholar
[5]Hall, Marshall Jr, The theory of groups, New York: (MacMillan), 1959.Google Scholar