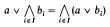Research Article
Models with second order properties in successors of singulars
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 122-137
-
- Article
- Export citation
Random models and the Maslov class
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 460-466
-
- Article
- Export citation
Near-equational and equational systems of logic for partial functions. I1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 795-827
-
- Article
- Export citation
A proof of morley's conjecture
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1346-1358
-
- Article
- Export citation
On the cofinality of the smallest covering of the real line by meager sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 828-832
-
- Article
- Export citation
The classification of excellent classes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1359-1381
-
- Article
- Export citation
An ideal characterization of Mahlo cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 467-473
-
- Article
- Export citation
Classification and interpretation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 138-159
-
- Article
- Export citation
Higher order reflection principles
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 474-489
-
- Article
- Export citation
Complementation in the Turing degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 160-176
-
- Article
- Export citation
Large resplendent models generated by indiscernibles
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1382-1388
-
- Article
- Export citation
Isols and the pigeonhole principle
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 833-846
-
- Article
- Export citation
Sacks forcing sometimes needs help to produce a minimal upper bound
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 490-498
-
- Article
- Export citation
Algorithmic information theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1389-1400
-
- Article
- Export citation
Generix strikes again
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 847-857
-
- Article
- Export citation
Models with the ω-property
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 177-189
-
- Article
- Export citation
Sequential theories and infinite distributivity in the lattice of chapters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 190-206
-
- Article
- Export citation
The consistency problem for positive comprehension principles
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1401-1418
-
- Article
- Export citation
A note on subgroups of the automorphism group of a saturated model, and regular types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 858-864
-
- Article
- Export citation
Inclusions et produits de groupes abéliens ordonnés étudiés au premier ordre
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 499-511
-
- Article
- Export citation

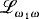 where
where 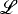 is countable. Although excellence arises in the study of the model theory of Scott sentences, it is not a dividing line in a classification of them. In particular, the assumption of nonexcellence does not yield much information. In fact, in [3] there is an example of a nonexcellent Scott sentence, categorical in ℵ
is countable. Although excellence arises in the study of the model theory of Scott sentences, it is not a dividing line in a classification of them. In particular, the assumption of nonexcellence does not yield much information. In fact, in [3] there is an example of a nonexcellent Scott sentence, categorical in ℵ
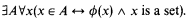
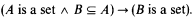

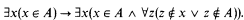
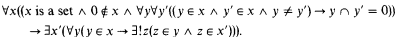
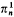 -indescribable cardinals for every
-indescribable cardinals for every 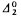 degree has a complement below 0′. We show that a 1-generic complement for each
degree has a complement below 0′. We show that a 1-generic complement for each 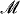 is a countable, recursively saturated model of PA, then for each infinite cardinal κ there is a resplendent
is a countable, recursively saturated model of PA, then for each infinite cardinal κ there is a resplendent 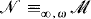 which has cardinality κ
which has cardinality κ