No CrossRef data available.
Article contents
Large resplendent models generated by indiscernibles
Published online by Cambridge University Press: 12 March 2014
Extract
The motivation for the results presented here comes from the following two known theorems which concern countable, recursively saturated models of Peano arithmetic.
(1) if 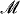 is a countable, recursively saturated model of PA, then for each infinite cardinal κ there is a resplendent
is a countable, recursively saturated model of PA, then for each infinite cardinal κ there is a resplendent 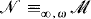 which has cardinality κ. (See Theorem 10 of [1].)
which has cardinality κ. (See Theorem 10 of [1].)
(2) if 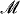 is a countable, recursively saturated model of PA, then
is a countable, recursively saturated model of PA, then 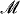 is generated by a set of indiscernibles. (See [4].)
is generated by a set of indiscernibles. (See [4].)
It will be shown here that (1) and (2) can be amalgamated into a common generalization.
(3) if 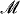 is a countable, recursively saturated model of PA, then for each infinite cardinal κ there is a resplendent
is a countable, recursively saturated model of PA, then for each infinite cardinal κ there is a resplendent 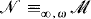 which has cardinality κ and which is generated by a set of indiscernibles.
which has cardinality κ and which is generated by a set of indiscernibles.
By way of contrast we will also get recursively saturated models of PA which fail to be resplendent and yet are generated by indiscernibles.
(4) if 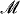 is a countable, recursively saturated model of PA, then for each uncountable cardinal κ there is a κ-like recursively saturated
is a countable, recursively saturated model of PA, then for each uncountable cardinal κ there is a κ-like recursively saturated 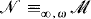 generated by a set of indiscernibles.
generated by a set of indiscernibles.
None of (1), (2) or (3) is stated in its most general form. We will make some comments concerning their generalizations. From now on let us fix a finite language L; all structures considered are infinite L-structures unless otherwise indicated.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1989


