Reviews
H. Poincaré. Science and hypothesis. With an Introduction by J. Larmor. Dover Publications, New York1952, xxvii + 244 pp. - Henri Poincaré. Science and method. Dover Publications, New York1952, 288 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 327
-
- Article
- Export citation
Research Article
Arithmetical problems and recursively enumerable predicates1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 33-41
-
- Article
- Export citation
On ω-inconsistency and a so-called axiom of infinity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 119-124
-
- Article
- Export citation
Note on a paradox
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 233
-
- Article
- Export citation
Strict implication, deducibility and the deduction theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 234-236
-
- Article
- Export citation
Reviews
Oskar Becker. Untersuchungen über den Modalkalkül. Westkulturverlag Anton Hain, Meisenheim am Glan1952, 87 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 327-329
-
- Article
- Export citation
Research Article
Investigation of the equivalence of the axiom of choice and Zorn's lemma from the viewpoint of the hierarchy of types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 125-135
-
- Article
- Export citation
Eine Bemerkung zu Henkin's Beweis für die Vollständigkeit des Prädikatenkalküls der ersten Stufe
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 42-48
-
- Article
- Export citation
The M-valued calculus of non-contradiction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 237-241
-
- Article
- Export citation
Certain predicates defined by induction schemata
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 49-59
-
- Article
- Export citation
Reviews
Oskar Anderson. Zur Axiomatik der Wahrscheinlichkeitslehre. Kontrolliertes Denken, Untersuchungen zum Logikkalkül und zur Logik der Einzelwissenschaften (Festschrift für Wilhelm Britzelmayr), edited by Albert Menne, Alexander Wilhelmy, and Helmut Angstl, rotaprint, Kommissions-Verlag Karl Alber, Munich1951, pp. 4–7.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 329
-
- Article
- Export citation
Research Article
Some formal relative consistency proofs
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 136-144
-
- Article
- Export citation
Systems of syntactic analysis
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 242-256
-
- Article
- Export citation
Inner models for set theory – Part III
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 145-167
-
- Article
- Export citation
Reviews
Helmut Angstl. Über Gleichungen im Aussagenkalkül. Kontrolliertes Denken, Untersuchungen zum Logikkalkül und zur Logik der Einzelwissenschaften (Festschrift für Wilhelm Britzelmayr), edited by Albert Menne, Alexander Wilhelmy, and Helmut Angstl, rotaprint, Kommissions-Verlag Karl Alber, Munich1951, pp. 8–9.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 329
-
- Article
- Export citation
Research Article
On the interpretation of the sign ‘⊃’
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 60-62
-
- Article
- Export citation
Conditioned disjunction as a primitive connective for the erweiterter Aussagenkalkül
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 63-65
-
- Article
- Export citation
Reviews
A. A. Markov. Konstruktivnaá logika (A constructive logic). Uspéhi matematičéskih nauk, vol. 5 no. 3 (1950), pp. 187–188.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 257
-
- Article
- Export citation
Walter Brugger. Die Übermodalität der Notwendigkeit in logischer Betrachtung. Kontrolliertes Denken, Untersuchungen zum Logikkalkül und zur Logik der Einzelwissenschaften (Festschrift für Wilhelm Britzelmayr), edited by Albert Menne, Alexander Wilhelmy, and Helmut Angstl, rotaprint, Kommissions-Verlag Karl Alber, Munich1951, pp. 18–21.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 329
-
- Article
- Export citation
Rudolf Carnap. The continuum of inductive methods. The University of Chicago Press, Chicago1952, v + 92 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 168-169
-
- Article
- Export citation

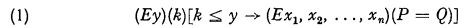
 and its relatives
and its relatives 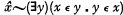 ,
, 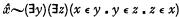 , and so on, correspondingly), are contradictions (
, and so on, correspondingly), are contradictions (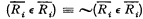 appears to obtain.
appears to obtain.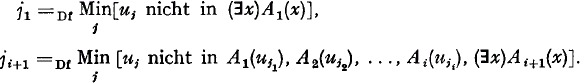
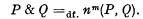
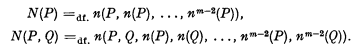
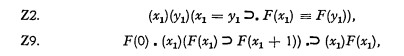
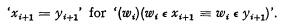
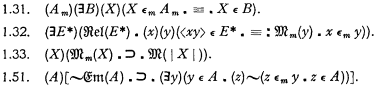
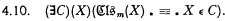

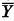 ) together with the logical constants
) together with the logical constants 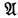 then (∃
then (∃