Article contents
Inner models for set theory – Part III
Published online by Cambridge University Press: 12 March 2014
Extract
In this third and last paper on inner models we consider some of the inherent limitations of the method of using inner models of the type defined in 1.2 for the proof of consistency results for the particular system of set theory under consideration. Roughly speaking this limitation may be described by saying that practically no further consistency results can be obtained by the construction of models satisfying the conditions of theorem 1.5, i.e., conditions 1.31, 1.32, 1.33, 1.51, viz.:
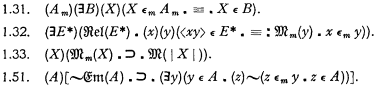
This applies in particular to the ‘complete models’ defined in 1.4. Before going on to a precise statement of these limitations we shall consider now the theorem on which they depend. This is concerned with a particular type of complete model examples of which we call “proper complete models”; they are those complete models which are essentially interior to the universe, those whose classes are sets of the universe constituting a class thereof, i.e., those for which the following proposition is true:
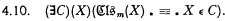
The main theorem of this paper is that the statement that there are no models of this kind can be expressed formally in the same way as the axioms A, B, C and furthermore it can be proved that if the axiom system A, B, C is consistent then so is the system consisting of axioms A, B, C, plus this new hypothesis that there exist no proper complete models. When combined with the axiom ‘V = L’ introduced by Gödel in (1) this new hypothesis yields a system in which any normal complete model which exists has for its universal class V, the universal class of the original system.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1953
References
BIBLIOGRAPHY
- 24
- Cited by


