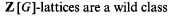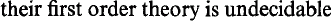Reviews
Barwise Jon and Moss Lawrence. Vicious circles. On the mathematics of non-wellfounded phenomena. CSLI lecture notes, no. 60. CSLI Publications, Stanford1996, also distributed by Cambridge University Press, New York, x + 390 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1039-1040
-
- Article
- Export citation
Yuri V. Matiyasevich. Hilbert's tenth problem. English translation of Desyataya problema Gil'berta, with a foreword by Martin Davis. Foundations of computing. The MIT Press, Cambridge, Mass., and London, 1993, xxii + 264 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 675-677
-
- Article
- Export citation
Research Article
An Ulm-type classification theorem for equivalence relations in Solovay model
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1333-1351
-
- Article
- Export citation
Reviews
Paul Horwich. Truth. Basil Blackwell, Oxford and Cambridge, Mass., 1990, xiii + 136 pp. - Marian David. Correspondence and disquotation. An essay on the nature of truth. Oxford University Press, New York and Oxford1994, x + 206 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 326-328
-
- Article
- Export citation
Hailperin Theodore. Sentential probability logic. Origins, development, current status, and technical applications. Lehigh University Press, Bethlehem, Pennsylvania, and Associated University Presses, London, 1996, 304 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1040-1041
-
- Article
- Export citation
Modality, morality, and belief, Essays in honor of Ruth Barcan Marcus, edited by Walter Sinnott-Armstrong, Diana Raffman, and Nicholas Asher, Cambridge University Press, Cambridge, New York, and Oakleigh, Victoria, 1995, xiii + 270 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 328-330
-
- Article
- Export citation
Yu. V. Matiyasevich. Desyataya problema Gil'berta. Russian original of the preceding. Matematicheskaya logika i osnovaniya matematiki. VO “Nauka,” Moscow1993, 223 pp. - Christos H. Papadimitriou. Computational complexity. Addison-Wesley Publishing Company, Reading, Mass., etc., 1994, xv + 523 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 677-678
-
- Article
- Export citation
Research Article
Scientific discovery based on belief revision
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1352-1370
-
- Article
- Export citation
Reviews
Probability and conditionals, Belief revision and rational decision, edited by Ellery Eells and Brian Skyrms, Cambridge studies in probability, induction, and decision theory, Cambridge University Press, Cambridge, New York, and Oakleigh, Victoria, 1994, viii + 207 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 330-335
-
- Article
- Export citation
Research Article
The complexity of the modal predicate logic of “true in every transitive model of ZF”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1371-1378
-
- Article
- Export citation
Reviews
Levi Isaac. For the sake of the argument. Ramsey test conditionals, inductive inference, and nonmonotonic reasoning. Cambridge University Press, Cambridge, New York, and Oakleigh, Victoria, 1996, xv + 341 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1041-1043
-
- Article
- Export citation
Advances in linear logic, edited by Jean-Yves Girard, Yves Lafont, and Laurent Regnier, London Mathematical Society lecture note series, no. 222, Cambridge University Press, Cambridge, New York, and Oakleigh, Victoria, 1995, vii + 389 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 678-680
-
- Article
- Export citation
Front matter
JSL volume 62 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Reviews
Øhrstrøm Peter and Hasle Per F. V.. Temporal logic. From ancient ideas to artificial intelligence. Studies in linguistics and philosophy, vol. 57. Kluwer Academic Publishers, Dordrecht, Boston, and London, 1995, viii + 413 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1044-1046
-
- Article
- Export citation
Research Article
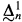 sets of reals
sets of reals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1379-1428
-
- Article
- Export citation
Reviews
Set theory, Annual Boise Extravaganza in Set Theory (BEST) conference, March 13–15, 1992, April 10–11, 1993, March 25–27,1994, Boise State University, Boise, Idaho, edited by Tomek Bartoszyński and Marion Scheepers, Contemporary mathematics, vol. 192, American Mathematical Society, Providence1996, xii + 184 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 680-683
-
- Article
- Export citation
Chris Mortensen. Inconsistent mathematics. Mathematics and its applications, vol. 312. Kluwer Academic Publishers, Dordrecht, Boston, and London, 1995, ix + 155 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 683-685
-
- Article
- Export citation
Back matter
JSL volume 62 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Reviews
Solvability, provability, definability: the collected works of Emil L. Post, edited by Davis Martin, Contemporary mathematicians, Birkhäuser, Boston, Basel, and Berlin, 1994, xxviii + 554 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1046-1048
-
- Article
- Export citation
Research Article
Wildness implies undecidability for lattices over group rings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1429-1447
-
- Article
- Export citation

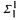 (resp.
(resp.  ) relation then the reduction above can be chosen in the class of all
) relation then the reduction above can be chosen in the class of all 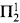 .
.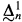 sets of reals
sets of reals
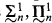 , and
, and 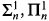 , and
, and 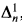 , we refer the reader to Moschovakis [19].
, we refer the reader to Moschovakis [19].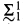 ) sets of reals are Lebesgue measurable and have the property of Baire.
) sets of reals are Lebesgue measurable and have the property of Baire.