No CrossRef data available.
Article contents
The complexity of the modal predicate logic of “true in every transitive model of ZF”
Published online by Cambridge University Press: 12 March 2014
Extract
Robert Solovay [8] investigated the version of the modal sentential calculus one gets by taking “□ϕ” to mean “ϕ is true in every transitive model of Zermelo-Fraenkel set theory (ZF).” Defining an interpretation to be a function * taking formulas of the modal sentential calculus to sentences of the language of set theory that commutes with the Boolean connectives and sets (□ϕ)* equal to the statement that ϕ* is true in every transitive model of ZF, and stipulating that a modal formula ϕ is valid if and only if, for every interpretation *, ϕ* is true in every transitive model of ZF, Solovay obtained a complete and decidable set of axioms.
In this paper, we stifle the hope that we might continue Solovay's program by getting an analogous set of axioms for the modal predicate calculus. The set of valid formulas of the modal predicate calculus is not axiomatizable; indeed, it is complete 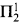 .
.
We also look at a variant notion of validity according to which a formula ϕ counts as valid if and only if, for every interpretation *, ϕ* is true. For this alternative conception of validity, we shall obtain a lower bound of complexity: every set which is 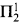 in the set of sentences of the language of set theory true in the constructible universe will be 1-reducible to the set of valid modal formulas.
in the set of sentences of the language of set theory true in the constructible universe will be 1-reducible to the set of valid modal formulas.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1997


