Research Article
A model complete theory of valued D-fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1758-1784
-
- Article
- Export citation
Subprevarieties versus extensions. Application to the logic of paradox
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 756-766
-
- Article
- Export citation
Hierarchies of monadic generalized quantifiers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1241-1263
-
- Article
- Export citation
Coordinatisation and canonical bases in simple theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 293-309
-
- Article
- Export citation
Supersimple ω-categorical groups and theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 767-776
-
- Article
- Export citation
The Logic of Choice
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1264-1310
-
- Article
- Export citation
Interpreting classical theories in constructive ones
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1785-1812
-
- Article
- Export citation
Logical questions concerning the μ-calculus: Interpolation, Lyndon and Łoś-Tarski
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 310-332
-
- Article
- Export citation
On fixed-point logic with counting
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 777-787
-
- Article
- Export citation
Two consistency results on set mappings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 333-338
-
- Article
- Export citation
Stationary sets and infinitary logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1311-1320
-
- Article
- Export citation
◇ at Mahlo cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1813-1822
-
- Article
- Export citation
The liar paradox and fuzzy logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 339-346
-
- Article
- Export citation
On representation theorems for nonmonotonic consequence relations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1321-1337
-
- Article
- Export citation
More on entangled orders
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1823-1832
-
- Article
- Export citation
Implicational F-structures and implicational relevance logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 788-802
-
- Article
- Export citation
Some applications of ordinal dimensions to the theory of differentially closed fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 347-356
-
- Article
- Export citation
Gödel sentences of bounded arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1338-1346
-
- Article
- Export citation
Minimal fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1833-1835
-
- Article
- Export citation
After all, there are some inequalities which are provable in ZFC
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 803-816
-
- Article
- Export citation

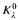 be the class of structures 〈
be the class of structures 〈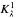 be the class of structures 〈
be the class of structures 〈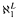 if
if 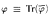 for all sentences φ? This problem is investigated in the frame of Łukasiewicz infinitely valued logic.
for all sentences φ? This problem is investigated in the frame of Łukasiewicz infinitely valued logic.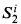 (
(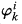 for Prf
for Prf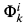 for PRF
for PRF