Research Article
A note on a theorem of Vaught
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 439-440
-
- Article
- Export citation
Simplifications of the recursion scheme
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 653-665
-
- Article
- Export citation
The generalized continuum hypothesis is equivalent to the generalized maximization principle1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 39-54
-
- Article
- Export citation
On theories categorical in their own power
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 240-244
-
- Article
- Export citation
On effectively discontinuous type-2 objects
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 245-248
-
- Article
- Export citation
Reviews
Reviews - Fred Sommers. The ordinary language tree. Mind, n.s. vol. 68 (1959), pp. 160–185. - Fred Sommers. Predicability. Philosophy in America, edited by Max Black, Cornell University Press, Ithaca1965, pp. 262–281. - L. R. Reinhardt. Dualism and categories. Proceedings of the Aristotelian Society, n.s. vol. 66 (1965), pp. 71–92. - David Massie. Sommers' tree theory, a reply to de Sousa. The Journal of philosophy, vol. 64 (1967), pp. 185–193. - Susan Haack. Equivocality, a discussion of Sommers' views. Analysis (Oxford), vol. 28 no. 5 (1968), pp. 159–165. - R. van Straaten. Sommers' rule and equivocality. Analysis (Oxford), vol. 29 no. 2 (1968), pp. 58–61. - Dan Passell. On Sommers' logic of sense and nonsense. Mind, n.s. vol. 78 (1969), pp. 132–133. - A. G. Elgood. Sommers' rules of sense. The philosophical quarterly, vol. 20 (1970), pp. 166–169.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 666-670
-
- Article
- Export citation
Research Article
On the notion of algebraic closedness for noncommutative groups and fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 441-444
-
- Article
- Export citation
ω-homomorphisms and ω-groups1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 55-65
-
- Article
- Export citation
Reviews
Lynn E. Rose. Aristotle's syllogistic. Charles C. Thomas, Publisher, Springfield, Illinois, 1968, vii + 149 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 670-671
-
- Article
- Export citation
Research Article
A minimal pair of Π10 classes1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 66-78
-
- Article
- Export citation
Incompleteness of a formal system for infinitary finite-quantifier formulas
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 445-455
-
- Article
- Export citation
A logic stronger than intuitionism1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 249-261
-
- Article
- Export citation
On strongly minimal sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 79-96
-
- Article
- Export citation
Two interpolation theorems for a
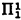 predicate calculus1
predicate calculus1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 262-270
-
- Article
- Export citation
Reviews
Judith Schoenberg. Belief and intention in the Epimenides. Philosophy and phenomenological research, vol. 30 no. 2 (1969), pp. 270–278.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 671-672
-
- Article
- Export citation
Research Article
A quasi-intumonistic set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 456-460
-
- Article
- Export citation
A remark on infinitary languages
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 461-462
-
- Article
- Export citation
Recursively enumerable sets which are uniform for finite extensions1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 271-287
-
- Article
- Export citation
Semantics for RKt1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 97-107
-
- Article
- Export citation
Reviews
Samuel Reiss. The universe of meaning. Philosophical Library, New York1953, xi + 227 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 672
-
- Article
- Export citation

 ), partial recursive in
), partial recursive in 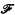 for the set of mappings from a subset of
for the set of mappings from a subset of 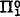 classes, where we proved the weaker result [2, Theorem 4.1] that the above pairs may be chosen so that
classes, where we proved the weaker result [2, Theorem 4.1] that the above pairs may be chosen so that 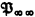 is the result of extending the basic predicate calculus
is the result of extending the basic predicate calculus 
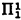 predicate calculus
predicate calculus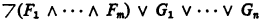
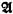 and
and 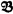 of powers
of powers 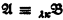 implies
implies 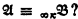 His proofs are by induction on the quantifier rank of formulas and they use an idea which in the case of ordinary first-order language goes back to Ehrenfeucht and Fraïssé. But, as we show, one can easily prove that if
His proofs are by induction on the quantifier rank of formulas and they use an idea which in the case of ordinary first-order language goes back to Ehrenfeucht and Fraïssé. But, as we show, one can easily prove that if