Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T17:37:55.175Z Has data issue: false hasContentIssue false
  • English
  • Français

Incompleteness of a formal system for infinitary finite-quantifier formulas

Published online by Cambridge University Press:  12 March 2014

John Gregory
John Gregory*
Affiliation:
University of Maryland, College Park, Maryland 20740
Get access Rights & Permissions [Opens in a new window]

Extract

In [1], various formal proof systems for infinitary formulas were defined. The formal proof system 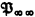is the result of extending the basic predicate calculus 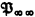by adding a collection Σ of axiom schemes and a collection Ω of rules of inference. Let Taut be the collection of all infinitary prepositional tautologies, considered as axiom schemes. Let ΩI consist of all the quantificational rules of independent choices. We will show, in §2 (see Theorem 2.1), that 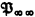(Taut; 0) is not complete for L∞ω (i.e., infinitary finite-quantifier) sentences; that is, we will exhibit an L∞ω sentence ϕ such that ¬ϕ is true in all models, but ¬ϕ is not provable in 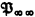(Taut; 0). (The unprovability is shown by a weak forcing version of Boolean general models.) This answers a question of Karp in [1,12.1(i)]. In §4, we will show that our ϕ is “ 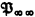complete for L∞ω ) sentences.”

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 36 , Issue 3 , September 1971 , pp. 445 - 455
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Karp, C. R., Languages with expressions of infinite length, North-Holland, Amsterdam, 1964.Google Scholar
[2]Karp, C. R., Nonaxiomatizability results for infinitary systems, this Journal, vol. 32 (1967), pp. 367–384.Google Scholar
[3]Levy, A., A hierarchy of formulas in set theory, Memoirs of the American Mathematical Society, no. 57 (1965).CrossRefGoogle Scholar
[4]Malitz, J., The Hanf number for complete Lω1ω sentences, The syntax and semantics of infinitary languages, Springer-Verlag, Berlin-Heidelberg-New York, 1968, pp. 166–181.CrossRefGoogle Scholar
[5]Sikorski, R., Boolean algebras, 2nd ed., Academic Press, New York, 1964.Google Scholar