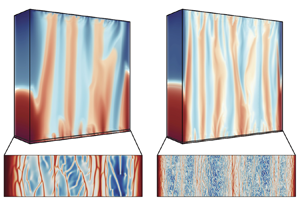
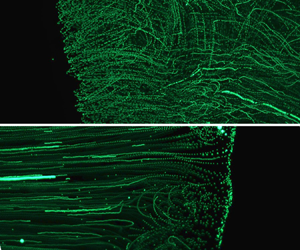
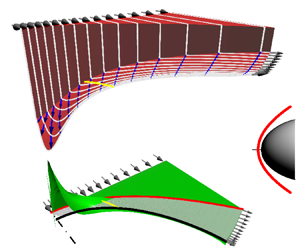
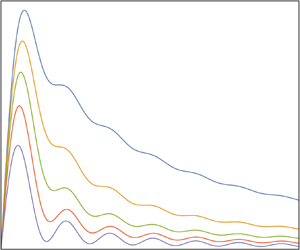
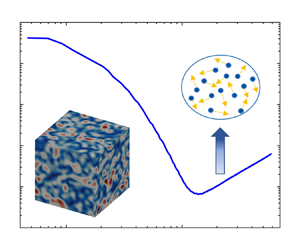
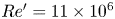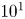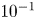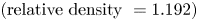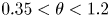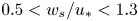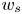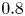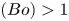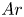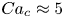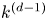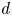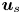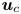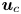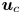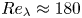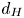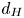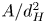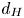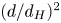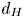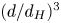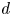doi:10.1017/jfm.2024.387 Liu et al. Turbulence and mixing from neighbouring stratified shear layers
JFM Papers
Stability of Stuart vortices in rotating stratified fluids
-
- Published online by Cambridge University Press:
- 16 May 2024, A12
-
- Article
-
- You have access
- HTML
- Export citation
Boundary-layer instability on a highly swept fin on a cone at Mach 6
-
- Published online by Cambridge University Press:
- 16 May 2024, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unifying constitutive law of vibroconvective turbulence in microgravity
-
- Published online by Cambridge University Press:
- 16 May 2024, A14
-
- Article
-
- You have access
- HTML
- Export citation
Role of volatility and thermal properties in droplet spreading: a generalisation to Tanner's law
-
- Published online by Cambridge University Press:
- 17 May 2024, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coexistence of dual wing–wake interaction mechanisms during the rapid rotation of flapping wings
-
- Published online by Cambridge University Press:
- 16 May 2024, A16
-
- Article
-
- You have access
- HTML
- Export citation
Investigating the parametric dependence of the impact of two-way coupling on inertial particle settling in turbulence
-
- Published online by Cambridge University Press:
- 16 May 2024, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fragmentation of colliding liquid rims
-
- Published online by Cambridge University Press:
- 16 May 2024, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The viscous force and torque on a closed irrotational surface
-
- Published online by Cambridge University Press:
- 16 May 2024, A19
-
- Article
-
- You have access
- HTML
- Export citation
Three-dimensional flow around and through a porous screen
-
- Published online by Cambridge University Press:
- 16 May 2024, A20
-
- Article
-
- You have access
- HTML
- Export citation
Impedance spectra of soft ionics
-
- Published online by Cambridge University Press:
- 17 May 2024, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Peristaltic pumping down a porous conduit
-
- Published online by Cambridge University Press:
- 17 May 2024, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Surface tension and wetting at free surfaces in smoothed particle hydrodynamics
-
- Published online by Cambridge University Press:
- 17 May 2024, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modelling the far-field effect of drag-induced dissipation in wave–structure interaction: a numerical and experimental study
-
- Published online by Cambridge University Press:
- 17 May 2024, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Turbulent kinetic energy budget of sediment-laden open-channel flows: bedload-induced wall-roughness similarity
-
- Published online by Cambridge University Press:
- 20 May 2024, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A study of streamline geometries in subsonic and supersonic regions of compressible flow fields
-
- Published online by Cambridge University Press:
- 20 May 2024, A26
-
- Article
-
- You have access
- HTML
- Export citation
Added mass of oscillating bodies in stratified fluids
-
- Published online by Cambridge University Press:
- 20 May 2024, A27
-
- Article
-
- You have access
- HTML
- Export citation
Bubble-induced entrainment at viscoplastic–Newtonian interfaces
-
- Published online by Cambridge University Press:
- 20 May 2024, A28
-
- Article
-
- You have access
- HTML
- Export citation
Effect of thermal fluctuations on spectra and predictability in compressible decaying isotropic turbulence
-
- Published online by Cambridge University Press:
- 21 May 2024, A29
-
- Article
-
- You have access
- HTML
- Export citation
Turbulent drag reduction with streamwise-travelling waves in the compressible regime
-
- Published online by Cambridge University Press:
- 21 May 2024, A30
-
- Article
-
- You have access
- HTML
- Export citation
Morphology of clean and surfactant-laden droplets in homogeneous isotropic turbulence
-
- Published online by Cambridge University Press:
- 22 May 2024, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation